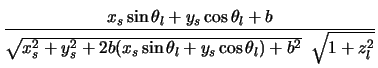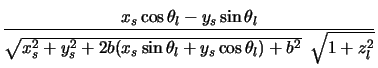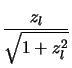Next: Gridded convolution
Up: Calculating the Line Profiles
Previous: Define the line of
The geometry2 subroutine
The geometry2 subroutine is called with 5 parameters: these are 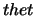 ,
,
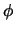 and the 3
co-ordinates for the offset position
for which the line of sight is to be calculated (x, y & z co-ordinates). It then proceeds to locate
the ring in the cloud in which this offset position is located. Then, using the same method as in the
geometry routine the line of sight from that position out of the cloud towards the observer is
divided into segments, one for each ring, for which the length and relative velocity are returned.
Unfortunately the vector describing the start point for this line of sight is not identical to the one used
previously (equation 4.8) as the lines of sight were previously defined as starting on (what we
are here calling) the y-axis, therefore
and the 3
co-ordinates for the offset position
for which the line of sight is to be calculated (x, y & z co-ordinates). It then proceeds to locate
the ring in the cloud in which this offset position is located. Then, using the same method as in the
geometry routine the line of sight from that position out of the cloud towards the observer is
divided into segments, one for each ring, for which the length and relative velocity are returned.
Unfortunately the vector describing the start point for this line of sight is not identical to the one used
previously (equation 4.8) as the lines of sight were previously defined as starting on (what we
are here calling) the y-axis, therefore 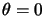 in equation 4.8. Therefore the new equation for
in equation 4.8. Therefore the new equation for
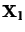 is
is
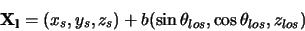 |
(4.49) |
where
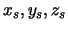 are the starting co-ordinates (in cartesians) of the line of sight. Note that as the x
and y axes are now swapped round4.19 compared to the previous use the
are the starting co-ordinates (in cartesians) of the line of sight. Note that as the x
and y axes are now swapped round4.19 compared to the previous use the
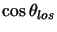 and
and
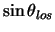 components are also reversed. Thus equation 4.10 describing the two possible intersections with a
particular cylinder is given by
components are also reversed. Thus equation 4.10 describing the two possible intersections with a
particular cylinder is given by
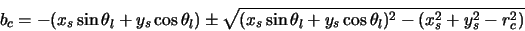 |
(4.50) |
The equation for finding the intersection with the disks is unchanged (equation 4.9).
For the same reasons the equations for finding the angles between the lines of sight and the velocity
components are also changed. The vectors for the velocity components (as in equation 4.14) are
So now taking the dot product of each of these in turn with equation 4.49 yields the required
three angles
There is also a midfind2 subroutine which performs the same functions as the
midfind
subroutine described in section 4.5.7. The equations are slightly modified,
mainly just involving the swapping round of the
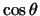 and
and
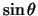 terms and to
take into account the non zero value of the y-co-ordinate for the starting position of the
line of sight. For example when calculating the point of closest approach to the
terms and to
take into account the non zero value of the y-co-ordinate for the starting position of the
line of sight. For example when calculating the point of closest approach to the 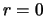 line,
equation 4.18 becomes
line,
equation 4.18 becomes
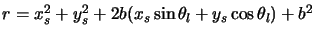 and thus differentiating this to find the value of
and thus differentiating this to find the value of 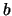 at the closest
approach yields the equivalent of equation 4.19 to be
at the closest
approach yields the equivalent of equation 4.19 to be





Next: Gridded convolution
Up: Calculating the Line Profiles
Previous: Define the line of
1999-04-12
![]() ,
,
![]() and the 3
co-ordinates for the offset position
for which the line of sight is to be calculated (x, y & z co-ordinates). It then proceeds to locate
the ring in the cloud in which this offset position is located. Then, using the same method as in the
geometry routine the line of sight from that position out of the cloud towards the observer is
divided into segments, one for each ring, for which the length and relative velocity are returned.
Unfortunately the vector describing the start point for this line of sight is not identical to the one used
previously (equation 4.8) as the lines of sight were previously defined as starting on (what we
are here calling) the y-axis, therefore
and the 3
co-ordinates for the offset position
for which the line of sight is to be calculated (x, y & z co-ordinates). It then proceeds to locate
the ring in the cloud in which this offset position is located. Then, using the same method as in the
geometry routine the line of sight from that position out of the cloud towards the observer is
divided into segments, one for each ring, for which the length and relative velocity are returned.
Unfortunately the vector describing the start point for this line of sight is not identical to the one used
previously (equation 4.8) as the lines of sight were previously defined as starting on (what we
are here calling) the y-axis, therefore ![]() in equation 4.8. Therefore the new equation for
in equation 4.8. Therefore the new equation for
![]() is
is