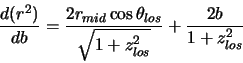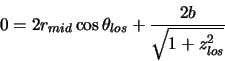The midfind subroutine

There is unfortunately one remaining problem. Consider first a line of sight that has $\theta=180^\circ$, this is the line of sight that runs exactly through the middle of the cloud. In a collapsing cloud this means that at the centre of the cloud the velocity field switches sign relative to the starting point of the line of sight. This means that the velocity field calculated for the innermost ring will be incorrect as it should really be considered as two separate rings, each with its own velocity (although the output from the geometry subroutine is correct as it is only for the cylinder or disk intersections with the line of sight the main program will then average these in pairs to get the velocity for each segment on the line of sight). Further consideration of this problem reveals that, depending on the type of velocity field specified, it potentially applies to all lines of sight. For example a line of sight with $\theta=160^\circ$ is quite likely to have a point somewhere where the velocity field changes sign. It is therefore necessary to check all lines of sight for this condition and if it does occur, split the line of sight segment into two sections and calculate the switchover position. It is also possible for there to be more than one velocity reversal if the line of sight passes through an outflow for example.

Once the geometry routine has calculated all the intersections along a line of sight it calls the midfind subroutine which compares the calculated values of the velocity component along the line of sight at each intersection. If there is a velocity reversal between two intersections then that segment is marked for later action.  

Once all the intersections have been checked those segments that were marked for action are each dealt with in turn in order to find the exact position for the velocity reversal. This is done by splitting each segment in half and calculating the velocity component at the mid point. It then takes the mid point and whichever end of the segment has a different sign for its velocity component and finds a new mid point (if the signs change then the changeover must be in that segment). It repeats this enough times to pin down the location of the switch over and force $vel3=0$. This point is then inserted into the $intersect$ array as though it were another intersection (all points occuring after it in the array are moved up one position so they are not overwritten). This effectively creates another segment on the line of sight which enables the main program to deal correctly with the velocity change. This is repeated for all segments on the line of sight that have velocity reversals.

The midfind subroutine also searches for the point on the line of sight closest to the centre line of the cloud. The reasons for this are given on page , only the method is explained here. The problem is to find the closest approach of the line given by ${\bf X_l}$ as in equation 4.8 to the line $r=0$. Let the line that joins the central line $r=0$ in the cloud to the line of sight in the $r-\theta$ plane be ${\bf X_{r\theta}}=(x_1,y_1,z)$. The points $x_1$ and $y_1$ are the co-ordinates of the intersection between the two lines and will be different for each $z$ (in most cases). The distance to the line $r=0$ for any given point on the line of sight is thus $r^2=x_1^2+y_1^2$. So now equating coefficients for ${\bf X_l}$ and ${\bf X_{r\theta}}$ we get two equations $r_{mid}+\frac{b}{\sqrt{1+z_{los}^2}}\cos \theta_{los}=x_1$ and $\frac{b}{\sqrt{1+z_{los}^2}}\sin \theta_{los} = y_1$. Squaring these and adding them together then gives the distance to the line r=0 (since $r^2=x_1^2+y_1^2$). So

$$r^2=r_{mid}^2+2\frac{b}{\sqrt{1+z_{los}^2}}r_{mid} \cos \theta_{los} + \left(\frac{b}{\sqrt{1+z_{los}^2}}\right)^2$$ (4.18)

The only variable here is $b$ so differentiating $r^2$ with respect to $b$ will yield the minimum value of $r$

$$\frac{d(r^2)}{db}=\frac{2r_{mid} \cos \theta_{los}}{\sqrt{1+z_{los}^2}} + \frac{2b}{1+z_{los}^2}$$

When this equals zero (ie. at the turning point)

$$0=2r_{mid} \cos \theta_{los}+\frac{2b}{\sqrt{1+z_{los}^2}}$$

and hence, finally. the required value of $b$ is given by

$$b_{close}= -(r_{mid} \cos \theta_{los}) \times \sqrt{1+z_{los}^2}$$ (4.19)

This is the value of $b$ at which the line of sight makes its closest approach to the $r=0$line in the cloud. This position is treated as described above and another point is inserted into the $intersect$ array.