Calculating the lines of sight

In a 1-D model it is only necessary to calculate the lines of sight in one half-plane. This half plane can then be integrated around the cloud and due to the symmetry of the situation is sufficient to calculate the radiation field at one point in the cloud due to all other shells in the cloud. This was formerly done by calculating just six lines of sight for each shell (the six lines were evenly spaced in $\cos \theta$within this half-plane). In a 2-D model there is no longer such a symmetry, in fact since the problem is not truly 2-D (i.e. not an infinitely long cylinder) there is no symmetry at all and it is necessary to treat this part of the problem in a fully 3-Dimensional way. The Cylindrical co-ordinate system   [r] It is first necessary to introduce the co-ordinate system used for this problem. In view of the 2-D symmetry that is being used cylindrical co-ordinates are the most appropriate choice. The origin of the co-ordinate system is taken as the intersection point of the line of symmetry with the lowest disk (ie. disk 0). Figure 4.3 shows such a setup with 5 cylinders (the planes are not shown to avoid cluttering the diagram). In a cylindrical co-ordinate system the 3 parameters are $(r,\theta,z)$ where, for an arbitrary point, $r$ is the distance from the $z$-axis, $\theta$ is the angle between the foot of the perpendicular and some arbitrary $x$-axis and $z$ is the length of the perpendicular. These 3 values are shown in Figure 4.3 for a general point. The z-axis is aligned along the centres of the cylinders. Due to the 2-D symmetry the position of the $\theta=0$-axis is not important as all possible locations for it are the same. The positions of the cylinders and disks can therefore be given by just one parameter each, this is stored in $cylloc$ and $diskloc$ respectively (with $cylloc(ncyls)$ and $diskloc(ndisks-1)$ representing the outermost cylinder and uppermost disk respectively, the lowest disk is $diskloc(0)$ and $cylloc(0)=0$is the central line of symmetry of the cloud).

The advantage of this co-ordinate system can be seen when the equations for the cylinders and planes are considered. A cylinder of radius $r_{c}$ is located at $\mathbf{X_c}=(r_{c},\theta,z) \hspace*{4mm} \forall \hspace*{1mm} \theta,z$. Similarly a disk at height $z_d$ above the origin is located at $\mathbf{X_d}=(r,\theta,z_d) \hspace*{4mm} \forall \hspace*{1mm} r,\theta$.

A straight line consisting of the combination of two vectors   [r] Unfortunately a straight line does not have such a simple expression. The general vector expression for a straight line is $\mathbf{X_l}=\mathbf{x_1}+b\mathbf{x_2}$. This is illustrated in Figure 4.4. The vector $\mathbf{x_1}$ (the dashed line with label $(r_1,\theta_1,z_1)$) points to any point on the required line (the thicker line). Then a fraction $b$ (which can be negative) of vector $\mathbf{x_2}$ is (the dashed line with label $(r_2,\theta_2,z_2)$) added to this point. Simply varying the value of $b$ will give any point on the line. However, in order to be able to simply add the individual components of vectors $\mathbf{x_1}$ and $\mathbf{x_2}$ it is necessary to use a co-ordinate system which has its axes perpendicular to one another, eg. the usual x,y,z arrangement. A general point $(r,\theta,z)$in cylindrical polars then becomes $(r\cos \theta,r\sin \theta,z)$ in Cartesians. The following equations therefore describe the planes, cylinders and lines:

$$\begin{array}{lll} {\rm plane:} & \mathbf{X_p}=(r_p \cos \the... ...s \theta_2 ,r_2 \sin \theta_2, z_2) & \forall b \\ \end{array}$$ (4.5)

Offcentre lines of sight   It can now be seen that the easiest position to consider lines of sight for is the origin as here the vector ${\bf x_1}$ is zero. Once the lines of sight at the origin have been calculated it is easy to calculate those at all other points in the cloud as the vector ${\bf x_1}$ will point to the position in the cloud of interest and the ${\bf x_2}$will simply be the same as the lines of sight at the origin. See figures 4.5 and 4.6 to help visualise this - figure 4.6 represents all the lines of sight at the origin (as described below) and figure 4.5 shows all these lines of sight offset by ${\bf X_1}$. This represents how the lines of sight would be drawn from the centre of one of the rings, where the centre of the ring has the offset ${\bf X_1}$.

The first part of the problem is how to space the lines of sight in a 3-D manner at the origin. Ideally it would be nice to space them evenly (i.e. the angle between any two lines of sight is the same). Unfortunately this is not possible, this problem is equivalent to asking whether it is possible to make a regular polyhedron with any given number faces (i.e. a platonic solid). A line of sight would pass through the middle of each face and all the lines of sight would then be evenly spaced. Unfortunately there are only 5 platonic solids^4.3 the largest of which has 20 sides. Although as will be shown in figures 5.26 & 5.27 using 20 lines of sight is in fact sufficient for the models used in this thesis it is quite possible that there are some models for which this is not the case. Note that using just 20 lines of sight leaves an angle of 52$^\circ$ degrees^4.4 between any two lines. In order to retain the flexibility to have as many lines of sight as desired the program has been written in a general manner that allows the user to specify the required number of lines of sight. However, this means that it is not possible to space the lines of sight evenly around the $4\pi$ steradians. However, as the number of lines increases it becomes less important if the lines are not perfectly spaced. Therefore the following method has been used.

Lines of sight   The number of lines to be evenly spaced around a great circle is given as an input called $hlines$, parameter $vlines$ then represents the number of positions perpendicular to this that are also to have lines of sight on them (note that this does not include the equatorial line). Figure 4.6 shows this with an example of $hlines=8$ (so here $vlines=2$). There are 8 horizontal lines of sight aligned along what could be termed the equator (marked by a dotted circle), there are then 2 other rings marked on the surface of the sphere (solid lines). These 2 circles together with a line at each pole and the dotted equatorial line give a total of 8 vertical positions for the lines of sight. This ensures an equal spacing vertically and horizontally. However, since the circles that are not on the equator are smaller than the equatorial circle there must be fewer lines of sight on these circles. There are $int(n_{\rm eq}\cos \phi)+1$ lines of sight on each circle where $n_{\rm eq}$ are the number of lines of sight on the equatorial circle and $\phi$ is the angle between the circle in question and the equatorial circle (i.e. $-\frac{\pi}{2} \leq \phi \leq \frac{\pi}{2}$). In this example $n_{\rm eq}=8$, $\phi=\frac{\pi}{4}$and so $int(n_{\rm eq}\cos \phi)+1=6$ as shown in figure 4.6 by the six dashed lines of sight pointing to each of the two solid rings. In addition there is also a single line pointing vertically upwards and a single line pointing vertically downwards. (ie. $\phi=\frac{\pi}{2}$ and $\phi=-\frac{\pi}{2}$) The general rule is that $hlines \in 4n$, $n\in \mathbb{Z} ^{+}$ and the example shown in figure 4.6 is in fact the minimum sensible number of lines of sight possible (ie. 22). The array $nlos$ stores the number of lines of sight for each `circle' on the sphere in figure 4.6, thus for the above example $nlos={8,8,6,6,1,1}$. Note that the first 8 is not needed as there is only one `equatorial' circle, however, to make the programming simpler it is calculated anyway.

Each line of sight is assigned a number (indexed by $counter$ in the program) and the co-ordinates for a vector of the form $(r,\theta,z)$ are stored in $tline(counter)=\theta$ and $zline(counter)=z$ (the two vertical lines are not actually vertical as this would need $zline=\infty$ so $zline$ is set to a very large number, presently 10,000). Due to the above mentioned point that $nlos$duplicates the number of lines of sight on the equatorial line the first $nlos(1)$ lines of sight are ignored - thus $counter$ labels the required lines of sight from $nlos(1)+1$ thru to $\sum_{i=1}^{2(vlines+1)}nlos(i)$. At the end of the geometry routine the labeling is altered to count lines of sight from 1 upwards to make it more logical for the rest of the program. Since $\theta$ is chosen as required there is no further calculation required for this value. If $r$ is always fixed at a certain value (say 1) then $z=r \tan \phi=\tan \phi$ where $\phi$ is the angle between the `equator' and the circle that the line of sight lies on. Thus

$${\bf x_2}=(1,\theta, \tan \phi)$$ (4.6)

These now represent the vectors ${\bf x_2}$for all positions in the cloud. It is now only necessary to find the different ${\bf x_1}$for each position in the cloud. These are chosen to be the middle of each ring. Thus if the cylinders are labelled $r_j$ and the disks $z_i$ for $j=0,\ldots,ncyls$ and $i=0,\ldots,ndisks$ (where $j=0$ represents the centre of the cylinders and $i=0$ the lowest disk in the cloud) the ring centres are at

$${\bf x_1}=(\frac{r_{j}+r_{j-1}}{2},0,\frac{z_i-z_{i-1}}{2})$$ (4.7)

($\theta$ is a free parameter due to the 2-D symmetry and is chosen to be zero for convenience). Thus the general line of sight is given (in cartesians) by

$${\bf X_l}={\bf x_1}+b{\bf x_2}=(r_{\rm mid},0,z_{\rm mid})+b(\cos \theta_{\rm los}, \sin \theta_{\rm los}, z_{\rm los})$$ (4.8)

where `mid' subscripts represent the co-ordinates of the mid point of a ring as in equation 4.7 and `los' subscripts label the parameters for a line of sight.

The task for the geometry subroutine is to take each line of sight at each position (i.e. equation 4.7 for $j=0,\ldots,ncyls$ and $i=0,\ldots,ndisks$ and equation 4.6 for all required values of $\theta$ and $\phi$) and calculate where that line of sight intersects other cylinders and rings on its way out of the cloud. In order to calculate where a particular line intersects a plane or cylinder consider equations 4.5 & 4.8. The line intersects a plane when ${\bf X_p=X_l}$. Thus equating the $z$ components of these 2 equations yields

$$b_p=\frac{z_p-z_{mid}}{z_{los}}$$ (4.9)

Similarly for the cylinder intersections ${\bf X_c=X_l}$ at the intersection point. Unfortunately it is not possible to equate the $z$ values here as this is a variable for the cylinders. It is therefore necessary to equate both the other parameters (ie. $r$ and $\theta$) to get

These can then be squared and added together to remove the $\theta_c$ and give

$$r_c^2=b^2+b2r_{mid}\cos \theta_{los}+r_{mid}^2$$

which is of course a quadratic in $b$ and can therefore be solved to give

$$b_c=-r_{mid} \cos \theta_{los} \pm \sqrt{r_{c}^2-r_{mid}^2 \sin^2 \theta_{los}}$$ (4.10)

So now the two possible values of $b$ are known (consider just the version of $b_c$ with the plus sign for the moment), the smaller of the two values will represent the first intersection. The distance to this intersection from the starting point (the middle of the ring being analysed) will be given by the magnitude of ${\bf x_2}$^4.5

$$\vert{\bf x_2}\vert=b\sqrt{1+z_{los}^2}$$ (4.11)

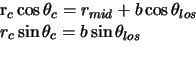
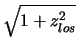where $b$ is the smaller of $b_p$ and $b_c$ (ie. it either intersects a plane at $b_p$ or a cylinder at $b_c$ first). Note that in the program the value of $\sqrt{1+z_{los}^2}$ is stored in variable $dist$. The program then repeats the above stages looking for the next intersection with a disk or a cylinder until it reaches the edge of the cloud. The array $intersect(counter,l,a)$ stores the results for each ring in the cloud with parameters in the following positions:

 

$counter$	line of sight counter
$l$	intersection number
in $a=1$	present ring x co-ordinate
in $a=2$	present ring y co-ordinate
in $a=3$	distance line of sight travels in present ring
in $a=4$	velocity of present ring relative
	to the origin of the line of sight
	(see section 4.5.4)

Originally the program was written with geometry routine called once at the beginning of the program and the entire geometry of the cloud was then calculated for each line of sight in each ring. However, for clouds with large numbers of disks and cylinders this leads to the intersect array becoming too large for present computers to easily handle. For example the old 1-D Sten models were usually run with 30 shells, to reproduce this kind of resolution in a cloud 30 cylinders and 60 disks are needed. This means that there can potentially be 120 intersections for a line of sight that travels diagonally across the cloud. Therefore the intersect array needs to have storage positions for 30 cylinders, 60 disks, 22 lines of sight (at a minimum) with 120 intersections and then the 4 parameters listed above for each intersection, ie. $30 \times 60 \times 120 \times 22 \times 4 = 19,008,000$ positions. This array needs to be double precision which assigns 8 bytes to each position, therefore the array needs approximately 152 MBytes of RAM, this increases to 704 Mbytes to reproduce a 50 shell model. These quantities of memory, whilst not impossible to provide, are expensive and led to consideration of methods of reducing these requirements. The method adopted therefore is that the geometry routine is called once for every ring in the cloud during each iteration. It then returns the geometry for each line of sight emanating in that ring. These data are then written over by the data from the next ring. This means that when the next iteration starts all these calculations are repeated for each ring. However, the original monolithic geometry routine took less than a minute to run so for a cloud that requires say 10 iterations to converge (this would be slow convergence, most clouds converge much faster) the time penalty is no more than 10 minutes which for a model that takes several hours to run anyway is an acceptable delay. Additionally since computers are able to handle small arrays much faster than they are large arrays there is an improvement in the speed at which the array contents are accessed. In the original STEN program a small part of the array storing the geometry information was used to calculate the line profiles at the end of the program. Making this array much smaller results in a large (factor of 10+) speed up for the line profile calculations. This is an effect that is worth considering for other parts of the program, ie. that it is paradoxically sometimes more efficient to re-calculate data than store it.

Lines of sight   Besides the above basic outline of the method there are additional complications that need to be considered in some situations. Firstly the matter of which sign to take in equation 4.10 was skipped over. Consideration of the situation for a general point in the cloud at $r_{mid}$ and its intersection with a cylinder at $r_{c}$ (see figure 4.7) shows that lines of sight which have

$$-r_{mid} \cos \theta_{los} > \sqrt{r_{c}^2-r_{mid}^2 \sin^2 \theta_{los}}$$

have two positive solutions. In other words they are similar to line 1 shown in figure 4.7 which first heads towards the centre of the cloud and therefore crosses the thickened cylinder twice. The program checks for this by calculating where the other intersection is (i.e. the other value of $b_c$ in equation 4.10). If both values are negative this represents the situation shown by line 3 where the solid cylinder is crossed twice but the negative values are on the dotted part of the line of sight (this represents the other solution for the equation of the line of sight but does not have a real meaning as the line of sight is only in one direction). If the two values of $b_c$ are equal this is the situation shown by line 2 which grazes the thickened cylinder. Here the program simply calculates two strips in the same cylinder which when added together give the total distance travelled in that cylinder (although the program does not add them together but simply stores two values for the same cylinder). Finally if the situation is as for line 1 then the program goes on to look again at both boundaries of the cylinder it finds itself in and again decides whether it is going in^4.6 or out. Once it decides it is going outwards the marker $noin$ (which is initially zero) is set equal to one and thereafter the program no longer checks the inward boundaries (since once it has started travelling outward it will never go in again).

The other situation that needs treating differently is the case where the lines of sight are horizontal (i.e. $z_{los}=0$) as in this case equation 4.9 involves dividing by zero. As this situation means that the line of sight will never cross any disk as it is lying parallel to them it is just necessary to calculate the intersections with the cylinders. Note that this problem does not directly arise for vertical lines, the infinite value appears in equation 4.11 where $z_{los}$ would become infinite for a vertical line, however, since $zline(counter)$ is never given an infinte number this problem does not arise (as was mentioned previously only near vertical lines are allowed).

It should also be noted that when a line exactly passes through a corner of two rings then due to rounding errors the program often includes a very short piece of a neighbouring ring in the line of sight. This will slightly slow the program down but due to the very short length in the other ring will not have a significant effect on the final output.