




Next: Calculating the lines of
Up: The geometry routine for
Previous: Introduction
This is the heart of the modification from the original 1-D stenholm program to the
present 2-D ASTRA program. The 1-D version consists of a series of concentric shells. In this 2-D
version the shells have been replaced by a system of disks and cylinders.
The model can be viewed as a series of concentric cylinders which are cut at
right angles by a series of planes, thus forming a set of stacked concentric rings each
with a rectangular cross-section. The model is that part of the total space that is bounded by the
lowest and uppermost plane and the outermost cylinder. This produces a cylindrical shaped model capped
by two flat disks.
Throughout the program it is necessary to refer to the rings, cylinders and disks by numbers and
therefore a consistent labelling system is important. The
cylinders are labelled from 1 to 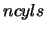 with label 0 being attached to the line of symmetry down the
centre of the cloud. The disks are labelled from 0 to
with label 0 being attached to the line of symmetry down the
centre of the cloud. The disks are labelled from 0 to 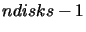 with 0 being the lowest disk and
with 0 being the lowest disk and 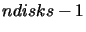 the uppermost. Thus there are
the uppermost. Thus there are 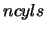 cylinders and
cylinders and 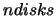 disks in the cloud.
The rings are labeled from 1 to
disks in the cloud.
The rings are labeled from 1 to
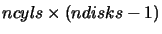 starting with the lowest and innermost ring and
then working outward and upward.
starting with the lowest and innermost ring and
then working outward and upward.





Next: Calculating the lines of
Up: The geometry routine for
Previous: Introduction
1999-04-12
![]() with label 0 being attached to the line of symmetry down the
centre of the cloud. The disks are labelled from 0 to
with label 0 being attached to the line of symmetry down the
centre of the cloud. The disks are labelled from 0 to ![]() with 0 being the lowest disk and
with 0 being the lowest disk and ![]() the uppermost. Thus there are
the uppermost. Thus there are ![]() cylinders and
cylinders and ![]() disks in the cloud.
The rings are labeled from 1 to
disks in the cloud.
The rings are labeled from 1 to
![]() starting with the lowest and innermost ring and
then working outward and upward.
starting with the lowest and innermost ring and
then working outward and upward.