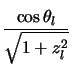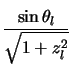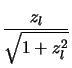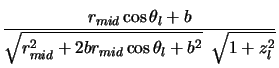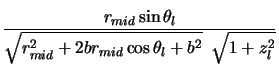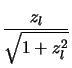Next: The midfind subroutine
Up: The geometry routine for
Previous: The givevel subroutine
Velocity components along the line of sight
[l]
![\includegraphics[scale=0.5]{losangle.eps}](img562.gif) Consider one particular line of sight which will be described by equation 4.8. This
is depicted in a 2-D version in figure 4.10 (ie. the z component is not shown). The figure shows just two rings
with the line of sight (labelled `los') and starting at position
Consider one particular line of sight which will be described by equation 4.8. This
is depicted in a 2-D version in figure 4.10 (ie. the z component is not shown). The figure shows just two rings
with the line of sight (labelled `los') and starting at position
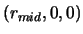 (ie. the
centre of the innermost ring). Two of the velocity components are shown (namely
(ie. the
centre of the innermost ring). Two of the velocity components are shown (namely
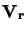 and
and
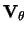 )
for the intersection with the outer edge of the second
ring and the line of sight vector,
)
for the intersection with the outer edge of the second
ring and the line of sight vector, 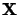 .
It is
necessary to calculate the components of each velocity vector that lies along the line of sight at each
intersection with a disk or a cylinder (as well as at the start of the line of sight). In order to
do this the angle between the line of sight and each component of velocity must be known.
This is best calculated using the definition of the dot product for vectors:
.
It is
necessary to calculate the components of each velocity vector that lies along the line of sight at each
intersection with a disk or a cylinder (as well as at the start of the line of sight). In order to
do this the angle between the line of sight and each component of velocity must be known.
This is best calculated using the definition of the dot product for vectors:
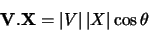 |
(4.12) |
where
Note that the length of 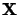 is unimportant for these purposes (ie. the value of
is unimportant for these purposes (ie. the value of 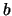 in
equation 4.8) as is the position (ie.
in
equation 4.8) as is the position (ie. 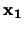 in equation 4.8) as it is
only the angle between this line and
in equation 4.8) as it is
only the angle between this line and 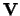 that is of interest.
that is of interest.
The vector 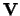 (the total velocity vector) takes on different forms depending on the location
along the line of sight for
which the angle is being calculated. At the origin of the line of sight it has components:
(the total velocity vector) takes on different forms depending on the location
along the line of sight for
which the angle is being calculated. At the origin of the line of sight it has components:
Note that these are the cylindrical co-ordinate system components, but their
components are given in cartesians (the dot product needs orthogonal axes to work).
For a general position along the line of sight the situation is more complex (these are the components
drawn in figure 4.10 - again the components are cartesians):
where 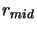 is the starting position for the line of sight and
is the starting position for the line of sight and 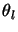 is the angle
of the line of sight (as previously defined). Now by picking the required value of
is the angle
of the line of sight (as previously defined). Now by picking the required value of 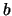 the
angle between the line of sight and the velocity components at any point on the line of sight
can be calculated. Using equations 4.13, 4.14 & 4.12 the solutions
are:
the
angle between the line of sight and the velocity components at any point on the line of sight
can be calculated. Using equations 4.13, 4.14 & 4.12 the solutions
are:
where the 1 subscript signifies the angle at the start of the line of sight. For the general case:
where the 2 subscript represents the angle at the desired end position on the line of sight.
So the velocity component along the line of sight is given by
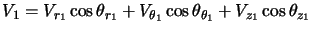 |
|
|
|
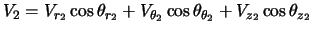 |
|
|
(4.17) |
The difference between these two values is the relative velocity between the start position of the line
of sight and the intersection of interest. This now means that each segment on the line of sight has its
velocity relative to the starting point of the line of sight defined at both ends. In the main program
these values will be averaged or interpolated to yield a relative velocity for the entire segment.





Next: The midfind subroutine
Up: The geometry routine for
Previous: The givevel subroutine
1999-04-12
![\includegraphics[scale=0.5]{losangle.eps}](img562.gif) Consider one particular line of sight which will be described by equation 4.8. This
is depicted in a 2-D version in figure 4.10 (ie. the z component is not shown). The figure shows just two rings
with the line of sight (labelled `los') and starting at position
Consider one particular line of sight which will be described by equation 4.8. This
is depicted in a 2-D version in figure 4.10 (ie. the z component is not shown). The figure shows just two rings
with the line of sight (labelled `los') and starting at position
![]() (the total velocity vector) takes on different forms depending on the location
along the line of sight for
which the angle is being calculated. At the origin of the line of sight it has components:
(the total velocity vector) takes on different forms depending on the location
along the line of sight for
which the angle is being calculated. At the origin of the line of sight it has components: