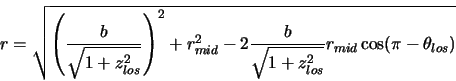![\includegraphics[scale=0.7]{velcalc.eps}](img539.gif)
The subroutine first works out in which ring the required point lies (it then knows which intersections
surround this point). Consider a point P (see figure 4.8) at co-ordinates ![]() ,
,
![]() which lie between cylinders
which lie between cylinders ![]() &
&
![]() and disks
and disks ![]() &
& ![]() (at co-ordinates
(at co-ordinates ![]() ,
,
![]() ,
,
![]() &
& ![]() respectively - ie.
cylinder/disk intersections A, B, C & D in the diagram). It
can then calculate the ratios of the distances between the disks and the cylinders, ie.
respectively - ie.
cylinder/disk intersections A, B, C & D in the diagram). It
can then calculate the ratios of the distances between the disks and the cylinders, ie.
![]() and
and
![]() .
Using these ratios the
.
Using these ratios the ![]() (ie. radial) component of velocity is calculated by first taking the two components at A & B and
combining them:
(ie. radial) component of velocity is calculated by first taking the two components at A & B and
combining them:
![]() and then the two components at C & D:
and then the two components at C & D:
![]() .
These two values can then be combined using
.
These two values can then be combined using ![]() to give
to give
![]() as the velocity component at point P. This procedure is then
repeated for the other two velocity components.
as the velocity component at point P. This procedure is then
repeated for the other two velocity components.
Finding the co-ordinates of a point in the cloud
[l]
![\includegraphics[scale=0.5]{btor.eps}](img554.gif) In order to be able to actually perform the above calculations it is of course necessary to first know the
absolute position in the cloud for which the velocity components are required. However, the positions along a
line of sight are defined in terms of the line of sight's starting position (
In order to be able to actually perform the above calculations it is of course necessary to first know the
absolute position in the cloud for which the velocity components are required. However, the positions along a
line of sight are defined in terms of the line of sight's starting position (![]() ), its direction
(
), its direction
(
![]() &
& ![]() )
and how far it has travelled so far (
)
and how far it has travelled so far (![]() ). Thus it is necessary to convert these
into
). Thus it is necessary to convert these
into ![]() and
and ![]() in the cloud's co-ordinates. Figure 4.9 demonstrates the problem. This is a top
view of a line of sight travelling at an angle of
in the cloud's co-ordinates. Figure 4.9 demonstrates the problem. This is a top
view of a line of sight travelling at an angle of ![]() - as defined earlier - (ie. effectively a
projection of the line of sight onto the plane of the disks). The
filled circle is the center line of the cloud (ie. the
- as defined earlier - (ie. effectively a
projection of the line of sight onto the plane of the disks). The
filled circle is the center line of the cloud (ie. the ![]() axis), the line of sight then starts at a distance
axis), the line of sight then starts at a distance
![]() from this centre line. After a distance
from this centre line. After a distance ![]() has been travelled along the line of sight the projection
distance
has been travelled along the line of sight the projection
distance ![]() will be
will be
![]() .
The problem is to find the distance
.
The problem is to find the distance ![]() that this
point is from the centre line of the cloud. Applying the cosine rule to this triangle yields the required
value:
that this
point is from the centre line of the cloud. Applying the cosine rule to this triangle yields the required
value: