![\includegraphics[scale=0.4]{gridpos.eps}](img739.gif) The fundamental problem to be solved is shown in figure 4.18. The telescope is located at
some angle relative to the centre line of symmetry in the cloud. When observing with the telescope observations of the cloud will be
made not just at the central position but also at various offset positions, often forming a grid of
observations. In the diagram for example 9 positions are shown. Offset positions are also required
when performing the gridded convolution necessary to simulate the telescope beam (which since it is not
infinitely small is spread off centre even when the telescope is pointing at the centre of the cloud - see
section 4.8.3).
These offset positions are referenced with
respect to the telescope's co-ordinate system (generally RA and Dec). This is, however, not the same
co-ordinate system as used in the cloud. The input files enable as many offset
positions as desired to be given for which output is to be produced. The offsets are given in arcseconds (as this is
generally what is used at the telescope) and are then translated by the program into distances within the
cloud. For example an offset of (15
The fundamental problem to be solved is shown in figure 4.18. The telescope is located at
some angle relative to the centre line of symmetry in the cloud. When observing with the telescope observations of the cloud will be
made not just at the central position but also at various offset positions, often forming a grid of
observations. In the diagram for example 9 positions are shown. Offset positions are also required
when performing the gridded convolution necessary to simulate the telescope beam (which since it is not
infinitely small is spread off centre even when the telescope is pointing at the centre of the cloud - see
section 4.8.3).
These offset positions are referenced with
respect to the telescope's co-ordinate system (generally RA and Dec). This is, however, not the same
co-ordinate system as used in the cloud. The input files enable as many offset
positions as desired to be given for which output is to be produced. The offsets are given in arcseconds (as this is
generally what is used at the telescope) and are then translated by the program into distances within the
cloud. For example an offset of (15
In order to calculate the line profile that a telescope would see it is necessary to know all the positions in the cloud that the line of sight passes through (this is done in the geometry2 subroutine - see section 4.8.2). In order to do this the vector components for the line of sight need to be translated from the co-ordinate sytem used by the telescope into the co-ordinate system used in the cloud. This is done in the prepgeom subroutine (prepare geometry).
The position of the observer relative to the cloud is defined in the input files with the parameters
Two co-ordinate systems
[l]
![\includegraphics[scale=0.7]{changcoord.eps}](img746.gif) Consider first the definition of a co-ordinate system. We have in this case a vector space
Consider first the definition of a co-ordinate system. We have in this case a vector space
![]() (ie. 3-D real space). A basis for a vector space is a linearly independent set which
spans it (p70, Griffel [11]). In this case the most obvious basis would be
(ie. 3-D real space). A basis for a vector space is a linearly independent set which
spans it (p70, Griffel [11]). In this case the most obvious basis would be
![]() {
{
![]() }. Stated formally, the problem here is that we have a vector
}. Stated formally, the problem here is that we have a vector
![]() (ie. the line of sight) stated with respect to the basis
(ie. the line of sight) stated with respect to the basis ![]() (ie. our co-ordinate
system as viewed by the telescope) but we wish to have the vector
(ie. our co-ordinate
system as viewed by the telescope) but we wish to have the vector ![]() stated with respect to the
basis
stated with respect to the
basis ![]() (ie. the co-ordinate system in the cloud). Each basis consists of 3 vectors (ie.
(ie. the co-ordinate system in the cloud). Each basis consists of 3 vectors (ie.
![]() and
and
![]() ). We already know
the
). We already know
the
![]() as they were defined above. To reduce the complexity as much as possible take
a cartesian co-ordinate system in the cloud with its origin at the same position as the origin of the
telescope based cartesian co-ordinate system. This is shown in figure 4.20. The
telescope co-ordinate system,
as they were defined above. To reduce the complexity as much as possible take
a cartesian co-ordinate system in the cloud with its origin at the same position as the origin of the
telescope based cartesian co-ordinate system. This is shown in figure 4.20. The
telescope co-ordinate system, ![]() ,
has axes
,
has axes ![]() and
and ![]() in the plane of the sky with
in the plane of the sky with ![]() being the
line between the centre of the cloud and the telescope with the positive direction being towards the
telescope. The origin of the system is the centre of the cloud. Similarly
the co-ordinate system in the cloud has its origin at the centre of the cloud: it is then however,
rotated
being the
line between the centre of the cloud and the telescope with the positive direction being towards the
telescope. The origin of the system is the centre of the cloud. Similarly
the co-ordinate system in the cloud has its origin at the centre of the cloud: it is then however,
rotated
![]() around the
around the ![]() axis (after this rotation the tips of the arrows point at
the dots in figure 4.20) and then
axis (after this rotation the tips of the arrows point at
the dots in figure 4.20) and then
![]() around the
around the ![]() axis. By
considering various triangles in figure 4.20 it is possible to deduce the relationship
between
axis. By
considering various triangles in figure 4.20 it is possible to deduce the relationship
between ![]() and
and ![]() :
:
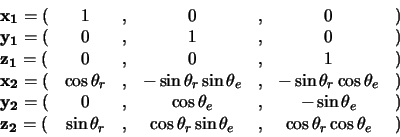
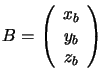 in basis
in basis 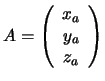 is its equivalent in basis
is its equivalent in basis
![]() is the change matrix and its entries are given by
is the change matrix and its entries are given by
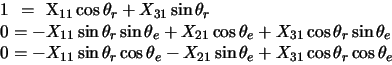
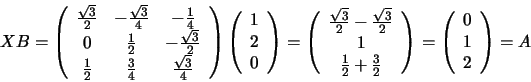
There is the possibility that the line of sight may exit the cloud through either the top or bottom disks.
This situation occurs when the z co-ordinate does not satisfy
![]() .
In this event it is
necessary to use equation 4.9 to find the intersection with the appropriate disk and then use
this point as the starting point for the line of sight.
.
In this event it is
necessary to use equation 4.9 to find the intersection with the appropriate disk and then use
this point as the starting point for the line of sight.
There is also the possibility that the line misses the cloud all together. This would be the case if a beam was
chosen to be so large that it covers the entire cloud - then some lines of sight in the beam may miss the cloud.
This case can be identified by there being no real solutions for ![]() in equation 4.46. This
situation arises when
in equation 4.46. This
situation arises when ![]() in which case the line of sight is assigned zero intensity.
in which case the line of sight is assigned zero intensity.
Line of sight direction
[l]
![\includegraphics[scale=0.4]{xproject.eps}](img803.gif) geometry2 also
needs to know the direction in which the line of sight is pointing. In the notation used in
equation 4.6 this means it needs a value for
geometry2 also
needs to know the direction in which the line of sight is pointing. In the notation used in
equation 4.6 this means it needs a value for ![]() (rotation angle) and
(rotation angle) and ![]() (the elevation
angle). This is shown in figure 4.21 where
(the elevation
angle). This is shown in figure 4.21 where ![]() is the
is the ![]() component of the line
of sight (ie. the line of sight shifted so that it passes through the origin) and
component of the line
of sight (ie. the line of sight shifted so that it passes through the origin) and ![]() is the
projection of this line onto the xy-plane.
is the
projection of this line onto the xy-plane. ![]() is then the angle between
is then the angle between ![]() and the y-axis
and
and the y-axis
and ![]() is the angle between
is the angle between ![]() and
and ![]() .
Because of the way the axis system was chosen (ie. the
.
Because of the way the axis system was chosen (ie. the ![]() -axis pointing at the telescope) the
lines of sight are all parallel to the telescope's
-axis pointing at the telescope) the
lines of sight are all parallel to the telescope's ![]() -axis4.17.
Therefore
-axis4.17.
Therefore
![]() in the telescope co-ordinates system and can be converted, using
equation 4.38, into
in the telescope co-ordinates system and can be converted, using
equation 4.38, into
![]() and therefore
and therefore
![]() in the cloud co-ordinate system4.18. The radial for the
in the cloud co-ordinate system4.18. The radial for the ![]() axis (ie. the
axis (ie. the
![]() -axis) is simply
-axis) is simply ![]() so using the
dot product (equation 4.12) on this and
so using the
dot product (equation 4.12) on this and ![]() gives
gives
| (4.48) |
Picking the correct value of ![]() [r]
[r]
![\includegraphics[scale=0.5]{thetsel.eps}](img816.gif)
Unfortunately there is an additional complication with equation 4.47 in that the
correct value of ![]() may lie between 180
may lie between 180![]() and 360
and 360![]() in which case the computer
will calculate the incorrect value of
in which case the computer
will calculate the incorrect value of ![]() .
The way around this is to check the
.
The way around this is to check the ![]() co-ordinates of the two points where the line of sight exits the cloud (ie. one on the near side and
one on the far side). If the far and near exit points are labelled
co-ordinates of the two points where the line of sight exits the cloud (ie. one on the near side and
one on the far side). If the far and near exit points are labelled ![]() and
and ![]() respectively then if
respectively then if
![]() the correct value will be
the correct value will be
![]() (where
(where ![]() is the value calculated in equation 4.47 above). Figure 4.22
demonstrates this graphically as a top view on the cloud. Two sample lines of sight are shown, in the
case of the dotted line the value of
is the value calculated in equation 4.47 above). Figure 4.22
demonstrates this graphically as a top view on the cloud. Two sample lines of sight are shown, in the
case of the dotted line the value of ![]() returned will be the correct value (ie.
returned will be the correct value (ie. ![]() )
as
the x-coordinate of the exit point closest to the telescope (positive y side of the cloud) is larger
than the x-coordinate of the exit point furthest away, ie.
)
as
the x-coordinate of the exit point closest to the telescope (positive y side of the cloud) is larger
than the x-coordinate of the exit point furthest away, ie. ![]() in the terminology used above.
For the dashed line, however,
in the terminology used above.
For the dashed line, however, ![]() and the program returns the value for
and the program returns the value for ![]() which must
be corrected as described above to yield
which must
be corrected as described above to yield ![]() .
.