




Next: Solving the Radiative Transfer
Up: The Lambda Iteration
Previous: The Lambda Iteration
In its original form the STEN program needed two arrays to describe the conditions in each shell, one giving
the value of the source function (this was stored in array s) and one giving the optical depth function
(stored in array kod). These were needed to be able to solve the radiative transfer equation
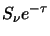 for a line of sight passing through that shell. It has already been shown (on
page
for a line of sight passing through that shell. It has already been shown (on
page ![[*]](icons/cross_ref_motif.gif) ) that the source function is given by
) that the source function is given by
![\begin{displaymath}S_\nu=\frac{2 h \nu^3}{c^2 \left[\frac{N_l g_u}{N_u g_l}-1\right]} \index{source function}
\end{displaymath}](img631.gif) |
(4.22) |
A similar equation is now needed for the optical depth function. Starting in the obvious place with the
absorption function (as in equation 2.26)
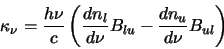 |
(4.23) |
Column density
![\includegraphics[scale=0.5]{gauss2.eps}](img633.gif) The
The
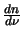 terms represent the rate of change of the number of molecules with frequency. In this
case they are distributed in a Gaussian form around the rest frequency of the photons emitted by the
molecules transitioning from the upper to the lower level. Figure 4.13 shows a Gaussian curve
centred on the rest frequency
terms represent the rate of change of the number of molecules with frequency. In this
case they are distributed in a Gaussian form around the rest frequency of the photons emitted by the
molecules transitioning from the upper to the lower level. Figure 4.13 shows a Gaussian curve
centred on the rest frequency 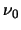 .
Any position that is offset from this maximum has a
intensity given by
.
Any position that is offset from this maximum has a
intensity given by
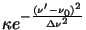 where
where
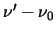 is the offset from the rest frequency
and
is the offset from the rest frequency
and 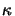 is the maximum value (ie. the value at the rest
frequency).
is the maximum value (ie. the value at the rest
frequency).
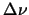 is the velocity width of the ring. The total number of molecules in a level is then given by
integrating
is the velocity width of the ring. The total number of molecules in a level is then given by
integrating
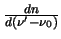 over the entire frequency range
over the entire frequency range
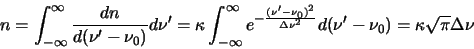 |
(4.24) |
where the final step here is a standard integral. So this gives
This can be converted to be in terms of a rest velocity using the Doppler relationship
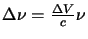 to give
to give
which can be substituted back into the original definition of
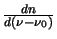 to give
to give
Note that since the function
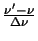 is dimensionless the units can be changed from frequency to velocity
with no effect. These equations can now in turn be used to convert equation 4.23 into the form
is dimensionless the units can be changed from frequency to velocity
with no effect. These equations can now in turn be used to convert equation 4.23 into the form
Using equation 2.23 one of the Einstein B coefficients can be removed. Also it is necessary to
apply a conversion factor to the Einstein B coefficient. This is because equation 4.23 is the
energy per unit frequency per unit volume but the definition of the Einstein B coefficients given in
section 2.1.1 was given in terms of the radiation intensity which is power per unit
frequency per unit solid angle per unit area. The conversion between these two different definitions of the
Einstein B coefficient is given by
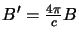 where
where 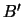 is the coefficient defined by the radiation
intensity (see section 2.1.1for the 2 definitions). Applying these two corrections then gives an
optical depth function of
is the coefficient defined by the radiation
intensity (see section 2.1.1for the 2 definitions). Applying these two corrections then gives an
optical depth function of
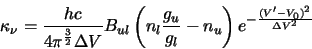 |
(4.25) |
When the program is actually solving the radiative transfer equation it will be using the form of equation 3.15.
This means that for every segment along a line of sight it multiplies the values of 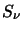 and
and
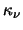 together. In certain
circumstances this can cause problems as the signs of
together. In certain
circumstances this can cause problems as the signs of 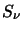 and
and
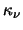 should always be the same, however if the
molecules are distributed such that
should always be the same, however if the
molecules are distributed such that
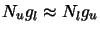 rounding errors in the computer may cause them to have different
signs. In order to avoid this problem a function called the emissivity function has been
defined4.8 such that
rounding errors in the computer may cause them to have different
signs. In order to avoid this problem a function called the emissivity function has been
defined4.8 such that
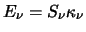 .
This then has the form
.
This then has the form
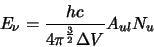 |
(4.26) |
Note that the 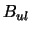 from equation 4.25 has been converted to
from equation 4.25 has been converted to 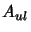 using
equation 2.24. This function is
used in the ASTRA program in place of the
using
equation 2.24. This function is
used in the ASTRA program in place of the
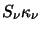 functions that appear in the STEN program (it is
referred to as
array eef in the program). Note also that the
functions that appear in the STEN program (it is
referred to as
array eef in the program). Note also that the
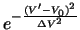 factor present in equation 4.25 has been removed in
equation 4.26. This must be done as this factor is different for each ring
depending on which line of sight is being dealt with and therefore needs to be calculated separately each time. The same factor
is also removed from the optical depth function given in equation 4.25 to give
factor present in equation 4.25 has been removed in
equation 4.26. This must be done as this factor is different for each ring
depending on which line of sight is being dealt with and therefore needs to be calculated separately each time. The same factor
is also removed from the optical depth function given in equation 4.25 to give
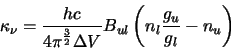 |
(4.27) |
This is the version stored in the array kod in the program.





Next: Solving the Radiative Transfer
Up: The Lambda Iteration
Previous: The Lambda Iteration
1999-04-12
![]() for a line of sight passing through that shell. It has already been shown (on
page
for a line of sight passing through that shell. It has already been shown (on
page ![]() ) that the source function is given by
) that the source function is given by
![\includegraphics[scale=0.5]{gauss2.eps}](img633.gif) The
The