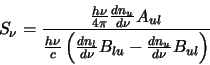Next: The LVG Approximation
Up: The radiative transfer equation
Previous: The radiative transfer equation
The Source Function
Any program that attempts to solve the radiative transfer equation needs some way of calculating the source
function. Using the definition in equation 3.2 and the expressions for
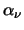 and
and 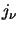 given in equations 2.25 & 2.26 gives
given in equations 2.25 & 2.26 gives
Now using the relationships between the Einstein coefficients given in
equations 2.23 & 2.24 this can be reduced to
![\begin{displaymath}
S_\nu=\frac{2h\nu^3}{c^2}\left[\frac{1}{\frac{g_u}{g_l}\frac{dn_l}{d\nu}\frac{d\nu}{dn_u}-1}\right]
\end{displaymath}](img313.gif) |
(3.7) |
The only remaining problem here is the
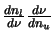 term which can be considered as
term which can be considered as
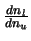 .
Differentiating equation 2.27 (the definition of excitation temperature)
shows that
.
Differentiating equation 2.27 (the definition of excitation temperature)
shows that
So substituting this into equation 3.7 finally yields
![\begin{displaymath}
S_\nu=\frac{2h\nu^3}{c^2}\left[\frac{1}{\frac{g_u}{g_l}\frac{n_l}{n_u}-1}\right]
\end{displaymath}](img317.gif) |
(3.8) |
1999-04-12
![]() and
and ![]() given in equations 2.25 & 2.26 gives
given in equations 2.25 & 2.26 gives