The LVG Approximation

Before describing the various methods for solving the radiative transfer problem in a general situation it is worth mentioning one approximation that is often used, namely the Large Velocity Gradient, or LVG, approximation. This is also more generally referred to as the Sobolev approximation. The Sobolev approximation assumes that only material with a Doppler shift of 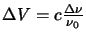$\Delta V = c \frac{\Delta \nu}{\nu_0}$ contributes to the emission at 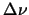$\Delta \nu$ [12]. More strictly in the sense required for the modelling of star formation regions it means that no two points in a cloud emit at the same frequency, or in other words, the emission at any point in the cloud is completely decoupled from emission at all other points in the cloud. In practice this requires an infalling or expanding cloud so that all points in the cloud have a different velocity.

Making this assumption greatly simplifies the problem since there is then no need to calculate the effect of radiation being absorbed and re-emitted on its way out of the cloud. Equally this of course means that the effects of radiation being re-absorbed can not be modelled (eg. self absorption). For the purposes of this thesis the main use of the approximation will be to test the results from a more general method of solving the radiative transfer equation.