The Monte Carlo Method

Besides what might be termed the 'brute force' method of solving the radiation transfer equation in a cloud using the Stenholm method (see section 3.5) there is also a statistical approach using Monte Carlo simulation. The application of Monte Carlo modelling to star formation modelling was first described in detail by Bernes [5]. It has since been expanded upon and developed into more complex programs capable of modelling 3-D objects by Juvela and Park & Hong [16,24,25]^3.1.

Given infinite computing power an excellent way of modelling a cloud would be to reproduce every molecule and every photon in a computer and then simulate their movement throughout the cloud. Unfortunately this requires more computing power than is ever likely to be available so some form of simplification is required. The basic principle behind the Monte Carlo method is to attempt to model the cloud by recreating a representative fraction of the photons in a cloud and tracing their motion. Clearly the more photons that can be followed the more accurate the results will be, but the longer a program will take to run. The technique described by Bernes [5] assigns each model photon to represent a large number of real photons. In a 3-D model a large number of cubes are stacked together to form one large cube (this is usually the case although there is no good reason why another shape - eg. a rectangle - may not be used except for the extra programming complications). Each cube has a certain number of model photons assigned to random locations within it which are then emitted in random directions. Each model photon has a weighting assigned to it which measures how many real photons it represents. The path of each model photon is traced through the cloud (ie. through the other cubes in its path) and its weighting is adjusted as it passes through each cube. The weighting will be adjusted downward to take into account absorption and upward to take into account stimulated emission. If there are considered to be $n_{i , l}$ and $n_{i , u}$ molecules per unit volume in levels $l$ and $u$respectively (with $u$ being the upper level and $l$ the lower level) in cube $i$ then there will be

$$N_i=n_{i , u}A_{ul}$$

spontaneous emissions per second in that cube where the $A_{ul}$ is the Einstein A coefficient (which is defined as the probability of spontaneous emission occurring in one second). To program this each cube is assigned a certain number of molecules depending on its location in the cloud. Some initial distribution amongst the levels is then assumed (ie. initial values of $n_{i , u}$ and $n_{i , l}$ are guessed at for all $u$ and $l$). These $N_i$ real photons will be represented by some $M_i$ model photons which will then be tracked - each model photon representing $\frac{N_i}{M_i}$ real photons. The model photons are assigned a frequency distribution $\phi(\nu)$ and can then be tracked through the cloud.

Each model photon travels a certain distance in its direction of motion and then the optical depth for that segment is calculated by

$$\tau_k=\frac{h\nu_{ul}}{4 \pi}\phi(\nu)(n_{i , l}B_{lu}-n_{i , u}B_{ul})s_k$$ (3.9)

where $B_{lu}$ and $B_{lu}$ are the Einstein absorption and stimulated emission coefficients respectively, $\nu_{ul}$ is the transition frequency, $h$ is Planck's constant and $s_k$ is the distance travelled. The subscript $k$ counts the segment number (ie. would be 1 for the first segment, 2 for the second, etc.). If the weight of the model photon was initially $W_0$ then after the first segment it becomes $W_0e^{-\tau_1}$. The total number of upward transitions stimulated by the photon for this segment is

$$N_{lu}=\frac{h\nu_{ul}}{4 \pi}\phi(\nu)n_{i , l}B_{lu}\int^{s_1}_{0}W(x)dx$$ (3.10)

If the volume of the cube is denoted as $V_i$ then the number of upward transitions per molecule in the cube stimulated by the photon is

$$S_{i , lu}=\frac{N_{lu}}{n_{i , l}V_i}$$ (3.11)

ie. the number of excitations caused by the photon divided by the number of molecules in the cube.

This process is repeated for each step along the direction of motion of the photon until the photon exits the cloud (this at least is the principle - in practice it may be more sensible to stop following the photon when its weight drops below a certain level representing when all the real photons it represents have been absorbed). Combining equations 3.9, 3.10 & 3.11 and using $W(x)=W_0e^{-\frac{\tau x}{s}}$ then yields the general equation describing the number of excitations per molecule in the i$^{\rm th}$ cube caused by the k$^{\rm th}$ step of the photon is given by

$$S_{i , lu}=\frac{h\nu_{ul}}{4 \pi}\phi(\nu)B_{lu}\frac{s_kW_0e^{-\sum^{k-1}_{i=1}\tau_i}}{V_i \, \tau_k} (1-e^{-\tau_k})$$

Thus, when all the model photons have been followed throughout the cloud then the total number of excitations and de-excitations in each cube is known and it is then possible to apply the statistical equilibrium equations in a similar manner as to that used in the Stenholm method (see section 4.7.3) to find the new level populations. The process is then re-started and continued in an iterative manner until the level populations converge on a final value.

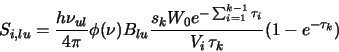
As would be expected the quality of the results depends on the number of model photons used and 'the random error in the results is approximately inversely proportional to the square root of the number of simulated photons' [16]. Thus significant improvements in accuracy require large increases in computing power. Generally on the order of 10$^5$-10$^6$ model photons are needed for modelling a 3-D cloud with somewhat less needed for 1-D modelling. The models run by Park & Hong used just over 14,000 cubes arranged to form a sphere (ie. a $31 \times 31 \times 31$ cube with the corners removed). Both Park & Hong and Juvela have thus far restricted themselves to studying the effects of clumpiness in clouds rather than the effects of non-spherically symmetric mass distribution and velocity that have been studied here.

There does not seem to be any overwhelming advantage of the Monte Carlo method over the Stenholm method except perhaps its proponents claim that it is easier to program. Its main disadvantage is that it is relatively computer intensive compared to the Stenholm method. It seems that the main benefit of having two completely different techniques is to increase confidence in the results if both methods give similar results.