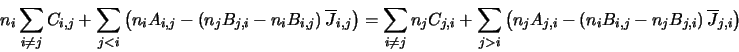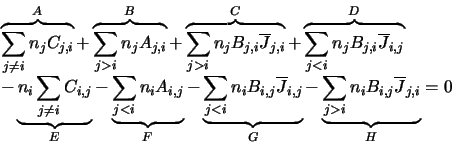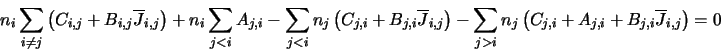Next: Calculating the level populations
Up: The Lambda Iteration
Previous: Solving the Radiative Transfer
Statistical Equilibrium
The aim here is to use the statistical equilibrium equation to calculate the new
level populations given the radiation field that has just been calculated in the main
program. The statistical equilibrium equations can be written (according to Athay [3])
as:
where 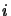 and
and 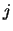 label the levels and take any valid level number. The
label the levels and take any valid level number. The 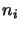 are the
level populations. The
are the
level populations. The 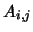 and
and 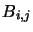 are, respectively the Einstein A and B
coefficients4.13.
The
are, respectively the Einstein A and B
coefficients4.13.
The
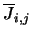 are the mean isotropic radiation field for any given
transition and the
are the mean isotropic radiation field for any given
transition and the 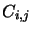 are the collision coefficients.
This can be expanded into its individual components to give:
are the collision coefficients.
This can be expanded into its individual components to give:
where, again, 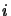 and
and 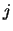 take values to cover all levels for which there are available
collision coefficients. The list below describes the different sections of this
equation:
take values to cover all levels for which there are available
collision coefficients. The list below describes the different sections of this
equation:
- A
- Molecules entering level
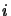 per second due to molecules leaving all other levels due to
collisions with
per second due to molecules leaving all other levels due to
collisions with 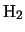 molecules.
molecules.
- B
- Molecules entering level
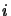 due to spontaneous emission from all higher levels.
due to spontaneous emission from all higher levels.
- C
- Molecules entering level
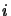 due to stimulated emission from all higher levels.
due to stimulated emission from all higher levels.
- D
- The number of molecules that enter level
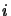 due to absorption
in all lower energy levels.
due to absorption
in all lower energy levels.
- E
- The number of molecules that leave level
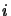 for any of the
other levels due to collisions with
for any of the
other levels due to collisions with 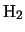 molecules.
molecules.
- F
- Molecules leaving level
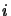 due to spontaneous emission into all lower levels.
due to spontaneous emission into all lower levels.
- G
- Molecules leaving level
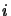 due to stimulated emission into all other lower
energy levels.
due to stimulated emission into all other lower
energy levels.
- H
- Molecules leaving level
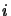 due to absorption into all higher levels.
due to absorption into all higher levels.
This can also be written (Matthews [20]) as:
This is the form that the program uses for its calculations.





Next: Calculating the level populations
Up: The Lambda Iteration
Previous: Solving the Radiative Transfer
1999-04-12