




Next: Solving the Matrix Equation
Up: Statistical Equilibrium
Previous: Statistical Equilibrium
In the program 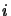 takes all values for which there are collision coefficients, thus
giving
takes all values for which there are collision coefficients, thus
giving 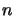 linear equations. However, there are only
linear equations. However, there are only 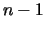 independent equations here as any
one equation will be contained in the other
independent equations here as any
one equation will be contained in the other 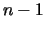 .
(This can be demonstrated by writing
out the two equations generated by allowing only 2 levels,
.
(This can be demonstrated by writing
out the two equations generated by allowing only 2 levels, 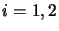 and adding them
together - they will equal zero and thereby be linearly dependent). Therefore the
program replaces one of the equations (the last one - but it could equally well replace any
other) with an equation representing the conservation of molecules
and adding them
together - they will equal zero and thereby be linearly dependent). Therefore the
program replaces one of the equations (the last one - but it could equally well replace any
other) with an equation representing the conservation of molecules
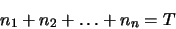 |
(4.30) |
where 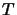 is the total number of molecules present.
In order to solve this series of linear equations it is necessary to write them as a
matrix of the form
is the total number of molecules present.
In order to solve this series of linear equations it is necessary to write them as a
matrix of the form
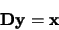 |
(4.31) |
The subroutine first fills the array elements 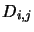 where
where 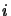 and
and 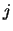 take values to
cover all levels. The array initially contains just the collision coefficients as it
enters the levels subroutine. To each element are then added numbers representing the
molecules entering and leaving the level as calculated in the main program:
take values to
cover all levels. The array initially contains just the collision coefficients as it
enters the levels subroutine. To each element are then added numbers representing the
molecules entering and leaving the level as calculated in the main program:
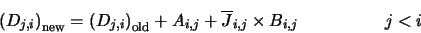 |
(4.32) |
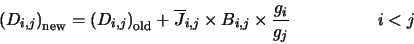 |
(4.33) |
where 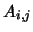 and
and 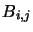 are, respectively, the Einstein A and B coefficients and
are, respectively, the Einstein A and B coefficients and
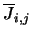 is the radiation intensity at the frequency of the
is the radiation intensity at the frequency of the
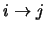 transition. Note that
transition. Note that
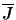 is represented in the program by the array BPL. Equation 4.32 fills all those array positions which represent
downward transitions and equation 4.33 fills all the array positions
representing upward transitions. The diagonal elements are then filled using
is represented in the program by the array BPL. Equation 4.32 fills all those array positions which represent
downward transitions and equation 4.33 fills all the array positions
representing upward transitions. The diagonal elements are then filled using
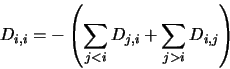 |
(4.34) |
The matrix 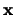 in equation 4.31 is filled with zeros except for position
in equation 4.31 is filled with zeros except for position 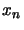 (where
(where 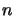 is the
highest level number) which contains the total number of molecules. This is for the
molecular conservation equation (equation 4.30) for which it is also necessary to replace all
the
is the
highest level number) which contains the total number of molecules. This is for the
molecular conservation equation (equation 4.30) for which it is also necessary to replace all
the 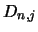 equations with the value one.
These
equations with the value one.
These 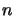 linear equations can now be represented by
linear equations can now be represented by
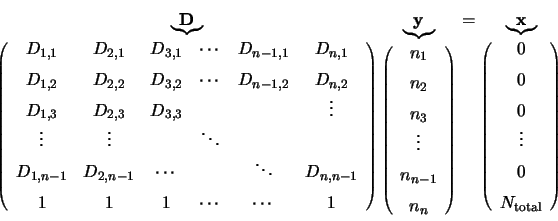 |
(4.35) |
It can now be seen why the values for the 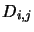 were set as they were by
equations 4.32, 4.33, 4.34. Consider one of the equations
given by this array system, say the third one:
were set as they were by
equations 4.32, 4.33, 4.34. Consider one of the equations
given by this array system, say the third one:
The terms
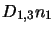 and
and
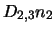 represent all molecules leaving level
represent all molecules leaving level 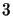 for
lower levels and
for
lower levels and 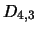 ,
,
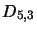 ,
...,
,
..., 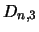 represent all molecules
leaving level
represent all molecules
leaving level 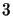 for higher levels.
for higher levels. 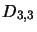 (which was calculated separately using
equation 4.34) represents all molecules entering level
(which was calculated separately using
equation 4.34) represents all molecules entering level 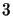 from all other
levels. Thus when all these terms are
added together the total number of molecules entering and leaving level
from all other
levels. Thus when all these terms are
added together the total number of molecules entering and leaving level 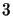 should be
equal and hence as
should be
equal and hence as 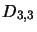 is negative the total is zero. Clearly the final line
simply sums the number of molecules in each level and sets this equal to the total
number of molecules in the system.
is negative the total is zero. Clearly the final line
simply sums the number of molecules in each level and sets this equal to the total
number of molecules in the system.
The next step is to solve this set of equations (ie. find the values of 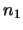 ,
,
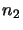 ,
...,
,
..., 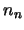 such that the equations are all true).
such that the equations are all true).





Next: Solving the Matrix Equation
Up: Statistical Equilibrium
Previous: Statistical Equilibrium
1999-04-12

![]() ,
,
![]() ,
...,
,
..., ![]() such that the equations are all true).
such that the equations are all true).