




Next: Convergence Check
Up: The Lambda Iteration
Previous: Calculating the level populations
Solving the Matrix Equation
In earlier versions of STEN this was done with the NAG routine F04ATF, however, as part
of the effort to remove all NAG routines from the program (in order to make it useable
on Linux systems for which NAG routines are not available) this has now been replaced
by a subroutine called matrix which solves this problem. It does this in several
stages. The matrices 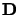 and
and 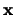 are then considered as a combined
augmented matrix and are placed in, first, echelon and then reduced echelon form (where all
entries other than the diagonals are zero) by the use of elementary matrix operations
(ie. adding a multiple of one line to another does not affect the
properties4.14 of the
matrix). This is also often referred to as Gaussian elimination. Each row of the matrix is then multiplied by the reciprocal of the leading
term (since the matrix is diagonalised this will be the entry on the diagonal). As this
too is an elementary matrix operation it does not affect the properties of the matrix.
These operations have now converted matrix
are then considered as a combined
augmented matrix and are placed in, first, echelon and then reduced echelon form (where all
entries other than the diagonals are zero) by the use of elementary matrix operations
(ie. adding a multiple of one line to another does not affect the
properties4.14 of the
matrix). This is also often referred to as Gaussian elimination. Each row of the matrix is then multiplied by the reciprocal of the leading
term (since the matrix is diagonalised this will be the entry on the diagonal). As this
too is an elementary matrix operation it does not affect the properties of the matrix.
These operations have now converted matrix 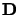 into an
into an
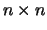 unit matrix
and have reduced the associated linear equations to the form
unit matrix
and have reduced the associated linear equations to the form
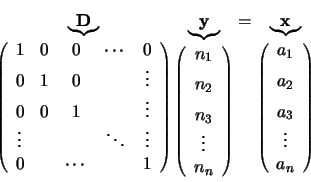 |
(4.36) |
where the 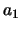 ,
,
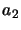 ,
...,
,
..., 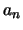 are the numbers generated by the above elementary
operations on the
are the numbers generated by the above elementary
operations on the 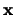 part of the augmented matrix.
part of the augmented matrix.
It can now be seen that since the 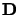 part of the matrix equation is a unit matrix
the values of
part of the matrix equation is a unit matrix
the values of 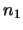 ,
,
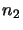 ,
...,
,
..., 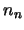 and
and 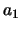 ,
,
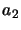 ,
...,
,
..., 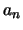 are
equivalent, ie.
are
equivalent, ie. 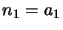 ,
,
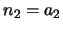 ,
...,
,
..., 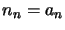 and these are the new level
populations for each of the
and these are the new level
populations for each of the 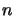 levels.
levels.
Using these level populations the new excitation temperature can be calculated using
equation 4.21. This whole procedure is then repeated for each shell. This is
then the end of the first iteration as the new excitation temperatures and population
levels have now been calculated for each shell throughout the entire cloud. The program
then performs a convergence check.





Next: Convergence Check
Up: The Lambda Iteration
Previous: Calculating the level populations
1999-04-12


![]() part of the matrix equation is a unit matrix
the values of
part of the matrix equation is a unit matrix
the values of ![]() ,
,
![]() ,
...,
,
..., ![]() and
and ![]() ,
,
![]() ,
...,
,
..., ![]() are
equivalent, ie.
are
equivalent, ie. ![]() ,
,
![]() ,
...,
,
..., ![]() and these are the new level
populations for each of the
and these are the new level
populations for each of the ![]() levels.
levels.