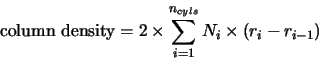Next: The Lambda Iteration
Up: Setting up the model
Previous: Setting up the model
Intersection/Ring relationship
![\includegraphics[scale=0.5]{ringnos.eps}](img610.gif) The parameter files store the values of the parameters for each intersection of the cylinders and disks
in the cloud, however, the program requires most of these values for each ring, not the intersections.
Therefore the program needs to convert the data from the files. In a 1-D model there is a fairly simple
relationship between the shell boundaries and the shells themselves since if there are
The parameter files store the values of the parameters for each intersection of the cylinders and disks
in the cloud, however, the program requires most of these values for each ring, not the intersections.
Therefore the program needs to convert the data from the files. In a 1-D model there is a fairly simple
relationship between the shell boundaries and the shells themselves since if there are 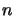 shells then
there are also
shells then
there are also 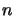 boundaries (or
boundaries (or 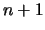 if the centre point of the cloud is counted). With a 2-D model
the connection is more difficult. Consider the example in figure 4.11: this shows a 3
cylinder by 6 disk model. The centre line of the cloud is the thicker line. If the rest of the diagram
is rotated around this centre line the cylinders and disks are formed (ie. this is a cross-section of
half the cloud). The convention used in the program is that the intersections and rings are labelled from
the bottom centre of the cloud outwards and upwards as shown. The relationship between the ring
numbers and the intersection numbers can be stated as4.7:
if the centre point of the cloud is counted). With a 2-D model
the connection is more difficult. Consider the example in figure 4.11: this shows a 3
cylinder by 6 disk model. The centre line of the cloud is the thicker line. If the rest of the diagram
is rotated around this centre line the cylinders and disks are formed (ie. this is a cross-section of
half the cloud). The convention used in the program is that the intersections and rings are labelled from
the bottom centre of the cloud outwards and upwards as shown. The relationship between the ring
numbers and the intersection numbers can be stated as4.7:
Any ring 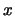 in a cloud with
in a cloud with 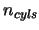 cylinders has four surrounding vertices given by:
cylinders has four surrounding vertices given by:
The parameter for a ring is then defined as the values at these 4 positions averaged together. This explains the rather
long statements describing each ring parameter in the program.
First the temperature in each ring is worked out. Once this is known the collision coefficients for each
transition can be worked out in each ring. This uses simple linear interpolation of the figures
provided for various temperatures in the COEFDATA.DAT file. At present the program can only
interpolate for temperatures that lie below the smallest temperature provided (ie. if a ring has a kinetic
temperature higher than the largest value listed in the COEFDATA.DAT file the program will stop). The
interpolation is a simple linear interpolation between the two surrounding temperatures for temperatures that
lie in the range for which collision coefficients are provided. For temperatures
below the lowest provided a linear decline between the two lowest temperatures provided is assumed and
continued down to the required temperature. The collision rate file
provides only the downward collision rates so the program has to calculate the upward
rates using the equation of detailed balance:
where i and j are the lower and upper levels respectively, the 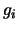 and
and 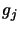 are the level
degeneracies (given by
are the level
degeneracies (given by 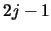 where
where 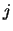 is the quantum number for that level),
is the quantum number for that level), 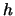 is
Planck's constant,
is
Planck's constant, 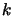 is Boltzman's constant,
is Boltzman's constant, 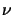 is the transition frequency and
is the transition frequency and
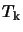 is the kinetic temperature.
is the kinetic temperature.
For each ring the full width at half maximum is calculated using the parameters for the turbulent
velocity given in the input file. From this the ring velocity width is calculated from
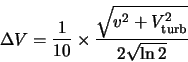 |
(4.20) |
and where
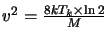 (with
(with 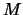 being the mass of the molecule). The factor of
being the mass of the molecule). The factor of
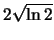 is due to the different definitions of
FWHM as explained next to figure 4.24.
is due to the different definitions of
FWHM as explained next to figure 4.24.
The program next calculates how many molecules there are in each ring and then makes a first guess at
how many of those molecules are in each excitation level. The
radiation intensity is set equal to that caused by the cosmic background radiation -
ie.
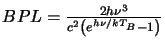 and
and 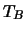 is set to
3 K (ie. the cosmic background temperature). The level populations can then be
calculated using the levels subroutine (see section 4.7.3). With the population levels
calculated the initial excitation temperature can be calculated for each ring. This
is done by re-arranging the definition of excitation temperature
is set to
3 K (ie. the cosmic background temperature). The level populations can then be
calculated using the levels subroutine (see section 4.7.3). With the population levels
calculated the initial excitation temperature can be calculated for each ring. This
is done by re-arranging the definition of excitation temperature
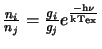 to give:
to give:
![\begin{displaymath}T_{\rm ex}=\frac{h \nu}{k}\frac{1}{\ln\left[\frac{n_jg_i}{n_ig_j}\right]} \index{temperature!excitation}
\end{displaymath}](img627.gif) |
(4.21) |
Column density
![\includegraphics[scale=0.3]{coldens.eps}](img628.gif) The column density is calculated simply by adding up the individual segments in each
ring for a line of sight that runs through the centre of the cloud out perpendicularly to the centre line
of the cloud (figure 4.12). Each ring's column density is easily calculated as the density in the ring and the length
of the line of sight segment is known. The figure returned is:
The column density is calculated simply by adding up the individual segments in each
ring for a line of sight that runs through the centre of the cloud out perpendicularly to the centre line
of the cloud (figure 4.12). Each ring's column density is easily calculated as the density in the ring and the length
of the line of sight segment is known. The figure returned is:
where 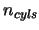 is the number of cylinders,
is the number of cylinders, 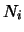 is the molecular density in the
is the molecular density in the
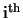 ring and
ring and 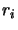 is the radius of the
is the radius of the
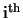 cylinder (with
cylinder (with 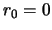 ).
Note that this is the column density right through the cloud (ie. not just to the
centre but effectively the total optical depth between the telescope and the edge of the universe).
).
Note that this is the column density right through the cloud (ie. not just to the
centre but effectively the total optical depth between the telescope and the edge of the universe).





Next: The Lambda Iteration
Up: Setting up the model
Previous: Setting up the model
1999-04-12
![\includegraphics[scale=0.5]{ringnos.eps}](img610.gif) The parameter files store the values of the parameters for each intersection of the cylinders and disks
in the cloud, however, the program requires most of these values for each ring, not the intersections.
Therefore the program needs to convert the data from the files. In a 1-D model there is a fairly simple
relationship between the shell boundaries and the shells themselves since if there are
The parameter files store the values of the parameters for each intersection of the cylinders and disks
in the cloud, however, the program requires most of these values for each ring, not the intersections.
Therefore the program needs to convert the data from the files. In a 1-D model there is a fairly simple
relationship between the shell boundaries and the shells themselves since if there are ![]() in a cloud with
in a cloud with ![]() cylinders has four surrounding vertices given by:
cylinders has four surrounding vertices given by:
![]() and
and ![]() is set to
3 K (ie. the cosmic background temperature). The level populations can then be
calculated using the levels subroutine (see section 4.7.3). With the population levels
calculated the initial excitation temperature can be calculated for each ring. This
is done by re-arranging the definition of excitation temperature
is set to
3 K (ie. the cosmic background temperature). The level populations can then be
calculated using the levels subroutine (see section 4.7.3). With the population levels
calculated the initial excitation temperature can be calculated for each ring. This
is done by re-arranging the definition of excitation temperature
![]() to give:
to give:
![\includegraphics[scale=0.3]{coldens.eps}](img628.gif) The column density is calculated simply by adding up the individual segments in each
ring for a line of sight that runs through the centre of the cloud out perpendicularly to the centre line
of the cloud (figure 4.12). Each ring's column density is easily calculated as the density in the ring and the length
of the line of sight segment is known. The figure returned is:
The column density is calculated simply by adding up the individual segments in each
ring for a line of sight that runs through the centre of the cloud out perpendicularly to the centre line
of the cloud (figure 4.12). Each ring's column density is easily calculated as the density in the ring and the length
of the line of sight segment is known. The figure returned is: