




Next: The Source Function
Up: Radiative Transfer Modelling
Previous: Radiative Transfer Modelling
Most of the work presented in this thesis involves the transportation of energy (as radiation) through a
medium, a process which is described by the equation of radiative transfer:
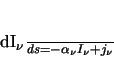 |
(3.1) |
where
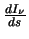 is the rate of change of radiation intensity,
is the rate of change of radiation intensity, 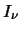 (at a particular
frequency
(at a particular
frequency 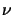 ), with distance,
), with distance, 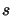 .
The rate at which it changes depends on the absorption coefficient
.
The rate at which it changes depends on the absorption coefficient
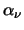 and the emission coefficient,
and the emission coefficient, 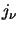 (these are defined as the absorption and emission per
unit length respectively). In order to provide a formal solution to this it will help to define optical depth
as:
(these are defined as the absorption and emission per
unit length respectively). In order to provide a formal solution to this it will help to define optical depth
as:
and the source function as:
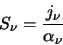 |
(3.2) |
This then enables equation 3.1 to be re-written as
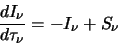 |
(3.3) |
This is now simply a first order differential equation which can be solved by the usual method of
multiplying by an integrating factor, in this case
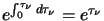 ,
to
give
,
to
give
Integrating both sides of equation 3.4 from zero to
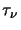 (ie. this represents
integrating along a line of sight from the edge of the universe to the observer) then gives
(ie. this represents
integrating along a line of sight from the edge of the universe to the observer) then gives
If 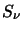 is assumed to be constant then this has the solution
is assumed to be constant then this has the solution
which can be re-arranged to give
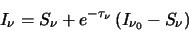 |
(3.5) |
where 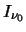 will usually represent the cosmic background radiation. When a telescope looks at a source it
sees it against the cosmic background radiation, in other words it will see
will usually represent the cosmic background radiation. When a telescope looks at a source it
sees it against the cosmic background radiation, in other words it will see
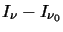 and thus the
observed intensity will be
and thus the
observed intensity will be
In an analogous way to equation 2.32 a temperature can be associated with this intensity, the
observed brightness temperature is the temperature above the background and is called the radiation
temperature, 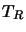
This has of course assumed that 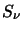 is not a function of
is not a function of 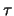 ,
in other words
,
in other words 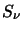 does not vary across the
cloud. This is an extremely restrictive assumption and in order to model a realistic cloud a way of solving
the radiative transfer equation for a variable
does not vary across the
cloud. This is an extremely restrictive assumption and in order to model a realistic cloud a way of solving
the radiative transfer equation for a variable 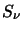 is necessary. Sections 3.3
and 3.5 describe the two main methods that have been used to tackle this problem.
is necessary. Sections 3.3
and 3.5 describe the two main methods that have been used to tackle this problem.





Next: The Source Function
Up: Radiative Transfer Modelling
Previous: Radiative Transfer Modelling
1999-04-12
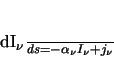
![]() is not a function of
is not a function of ![]() ,
in other words
,
in other words ![]() does not vary across the
cloud. This is an extremely restrictive assumption and in order to model a realistic cloud a way of solving
the radiative transfer equation for a variable
does not vary across the
cloud. This is an extremely restrictive assumption and in order to model a realistic cloud a way of solving
the radiative transfer equation for a variable ![]() is necessary. Sections 3.3
and 3.5 describe the two main methods that have been used to tackle this problem.
is necessary. Sections 3.3
and 3.5 describe the two main methods that have been used to tackle this problem.