




Next: The James Clerk Maxwell
Up: Observing Star Formation Regions
Previous: Temperature Definitions
The previous sections have described in some detail the process in which molecules emit radiation, however, in
astronomy the key objective is the detection of this radiation after it has travelled the huge distances between
the emission source and the Earth. For the types of object being described here the radiation will have
typically travelled anywhere between a few hundred and a few thousand parsecs. Therefore the signal received
on Earth even by a large telescope will be extremely weak. The operation of a typical radio telescope (the
JCMT) will be described in the next section. This section will concentrate on the methods used to describe the
signals received.
At its most basic level the telescope counts the photons that fall on the dish2.3. These photons carry a certain amount of energy which defines their frequency (via 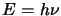 ). The
receiver on the telescope is capable of counting photons at a particular frequency and can therefore tell how
much energy is received at that frequency. Most detectors do not actually return a reading saying how
many photons have been detected but rather enable the total energy collected to be measured. This is known as
the radiation intensity, generally denoted
). The
receiver on the telescope is capable of counting photons at a particular frequency and can therefore tell how
much energy is received at that frequency. Most detectors do not actually return a reading saying how
many photons have been detected but rather enable the total energy collected to be measured. This is known as
the radiation intensity, generally denoted 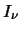 or
or 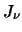 (the
(the 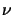 because it is at a specific
frequency,
because it is at a specific
frequency, 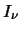 is generally the actual intensity of a source and
is generally the actual intensity of a source and 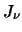 is generally the observed
intensity). This is defined as the amount of energy received (or transmitted) per unit area, per solid angle,
per unit frequency, per second (ie.
is generally the observed
intensity). This is defined as the amount of energy received (or transmitted) per unit area, per solid angle,
per unit frequency, per second (ie.
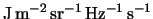 ).
).
The total luminosity of a source (generally 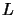 )
is the total power output of a source (ie. is measured simply
in Watts). At a distance,
)
is the total power output of a source (ie. is measured simply
in Watts). At a distance, 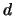 ,
from a point source the flux may be defined as the power passing through a unit
area. Assuming the source emits isotropically this is the luminosity of the source divided by the surface
area of a sphere of radius
,
from a point source the flux may be defined as the power passing through a unit
area. Assuming the source emits isotropically this is the luminosity of the source divided by the surface
area of a sphere of radius 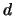 ,
ie.
,
ie.
This can of course also be written as a frequency, specificaly as
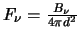 where
where 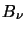 is the
luminosity per unit frequency and is thus related to the total luminosity by
is the
luminosity per unit frequency and is thus related to the total luminosity by
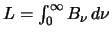 .
This in turn can be related to the radiation intensity by
.
This in turn can be related to the radiation intensity by
where the integral is over the solid angle of the source. Note that 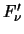 will only be exactly the same as
will only be exactly the same as 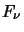 for a point source, however, as long as the source subtends a 'small' solid angle as viewed by a telescope
they will be approximately the same.
for a point source, however, as long as the source subtends a 'small' solid angle as viewed by a telescope
they will be approximately the same.
If the source is a black body then the radiation intensity will depend only on the source's excitation temperature and
will be given by the Planck function
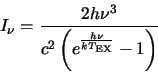 |
(2.28) |
From this the brightness temperature is defined by applying the Rayleigh-Jeans approximation that
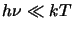 so that
so that
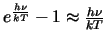 to give
to give
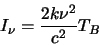 |
(2.29) |
Note that since this is the definition of brightness temperature it is unimportant whether the Rayleigh-Jeans
approximation holds or not (and it is not valid for radio wavelengths). Since equations 2.30
and 2.31 are both a measure of the observed intensity they can be set equal to each other to give
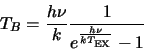 |
(2.30) |
This is the definition of the observed intensity (ie. 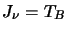 ).
).





Next: The James Clerk Maxwell
Up: Observing Star Formation Regions
Previous: Temperature Definitions
1999-04-12
![]() ). The
receiver on the telescope is capable of counting photons at a particular frequency and can therefore tell how
much energy is received at that frequency. Most detectors do not actually return a reading saying how
many photons have been detected but rather enable the total energy collected to be measured. This is known as
the radiation intensity, generally denoted
). The
receiver on the telescope is capable of counting photons at a particular frequency and can therefore tell how
much energy is received at that frequency. Most detectors do not actually return a reading saying how
many photons have been detected but rather enable the total energy collected to be measured. This is known as
the radiation intensity, generally denoted ![]() or
or ![]() (the
(the ![]() because it is at a specific
frequency,
because it is at a specific
frequency, ![]() is generally the actual intensity of a source and
is generally the actual intensity of a source and ![]() is generally the observed
intensity). This is defined as the amount of energy received (or transmitted) per unit area, per solid angle,
per unit frequency, per second (ie.
is generally the observed
intensity). This is defined as the amount of energy received (or transmitted) per unit area, per solid angle,
per unit frequency, per second (ie.
![]() ).
).
![]() )
is the total power output of a source (ie. is measured simply
in Watts). At a distance,
)
is the total power output of a source (ie. is measured simply
in Watts). At a distance, ![]() ,
from a point source the flux may be defined as the power passing through a unit
area. Assuming the source emits isotropically this is the luminosity of the source divided by the surface
area of a sphere of radius
,
from a point source the flux may be defined as the power passing through a unit
area. Assuming the source emits isotropically this is the luminosity of the source divided by the surface
area of a sphere of radius ![]() ,
ie.
,
ie.