




Next: Temperature Definitions
Up: The Theory Of Spectral
Previous: The Theory Of Spectral
Einstein Coefficients
Kirchoff's Law,
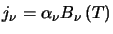 ,
states that for a
material whose emission is solely a function of its temperature, its emission must equal
its absorption in equilibrium. Whilst considering this, Einstein realised that this
implied a statistical relationship between the emission and absorption of individual
levels in the molecules of the material. He initialy considered just two energy levels, separated
by an energy of
,
states that for a
material whose emission is solely a function of its temperature, its emission must equal
its absorption in equilibrium. Whilst considering this, Einstein realised that this
implied a statistical relationship between the emission and absorption of individual
levels in the molecules of the material. He initialy considered just two energy levels, separated
by an energy of 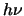 ,
in a radiation field
,
in a radiation field
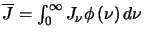 where
where 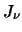 is the radiation at a particular frequency and
is the radiation at a particular frequency and
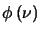 ,
the line profile function, is normalised as
,
the line profile function, is normalised as
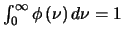 .
.
- Spontaneous Emission:
- When in level 2 the molecule has a probability of
spontaneously releasing a photon (of energy
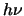 )
and transitioning to level 1. This
probability is denoted by
)
and transitioning to level 1. This
probability is denoted by 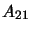 ,
the Einstein A coefficient and is usually given in
units of probability per second of a molecule transitioning. Note that
,
the Einstein A coefficient and is usually given in
units of probability per second of a molecule transitioning. Note that 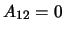 since if
this were not the case it would imply the molecule was gaining energy from nothing.
since if
this were not the case it would imply the molecule was gaining energy from nothing.
- Stimulated Emission
- Spontaneous emission takes place in the absence of a radiation
field, however, if one is present then the radiation can stimulate a molecule in level 2
to emit a photon (energy
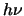 )
and transition to level 1. This is stimulated
emission and is denoted by
)
and transition to level 1. This is stimulated
emission and is denoted by
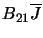 and is also usually given as probability
of a transition occurring for one molecule per second.
and is also usually given as probability
of a transition occurring for one molecule per second. 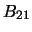 is one of the Einstein B
coefficients.
is one of the Einstein B
coefficients.
- Absorption
- The third method of transitioning also requires a radiation field and
is where a molecule in level 1 absorbs a photon of energy
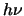 and thereby transitions
to level 2. The probability of this occurring is
and thereby transitions
to level 2. The probability of this occurring is
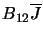 again usually the
probability of a transition occurring for one molecule per second.
again usually the
probability of a transition occurring for one molecule per second. 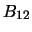 is the second
Einstein B coefficient.
is the second
Einstein B coefficient.
Clearly, if the system is in equilibrium then the number of molecules leaving one level
must equal the number entering it so the three coefficients are linked by
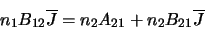
where 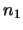 and
and 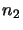 are the number of molecules in level 1 and level 2 respectively. Note that this assumes
that the density is sufficiently low that no collisions take place (which could otherwise induce transitions).
This can also be re-arranged to give
are the number of molecules in level 1 and level 2 respectively. Note that this assumes
that the density is sufficiently low that no collisions take place (which could otherwise induce transitions).
This can also be re-arranged to give
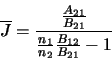
The ratio of the level populations can be replaced by
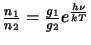 (the ratio of the level populations in thermodynamic equilibrium) thus giving
(the ratio of the level populations in thermodynamic equilibrium) thus giving
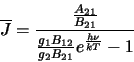
However, in thermodynamic equilibrium the radiation field will be equal to the Planck function (ie.
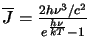 )
which implies that
)
which implies that
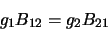 |
(2.21) |
and
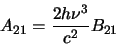 |
(2.22) |
where 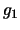 and
and 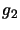 are the degeneracies for level 1 and 2 respectively (the number of ways the angular
momentum, J, may be orientated in space - equal to
are the degeneracies for level 1 and 2 respectively (the number of ways the angular
momentum, J, may be orientated in space - equal to 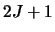 ). The Einstein
coefficients are properties of a particular molecule and as equations 2.23
and 2.24 contain
only the coefficients and some physical constants they are independent of the conditions
in which the molecules find themselves (ie. specifically, they hold even if the molecules are not in
thermodynamic equilibrium).
). The Einstein
coefficients are properties of a particular molecule and as equations 2.23
and 2.24 contain
only the coefficients and some physical constants they are independent of the conditions
in which the molecules find themselves (ie. specifically, they hold even if the molecules are not in
thermodynamic equilibrium).
Unfortunately there are two possible definitions of the Einstein B coefficients depending upon whether the emission is due to the
local radiation intensity or the local energy density. Equation 2.24 above is for radiation intensity case, the
equivalent equation for emission due to energy density is
Care needs to be taken over which definition is being used to avoid problems caused by the factor of
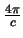 difference.
difference.
It is now possible to define an emission coefficient which can be seen as the energy per transition (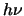 )
multiplied by a function that measures the rate of change of the upper level population with frequency
(
)
multiplied by a function that measures the rate of change of the upper level population with frequency
(
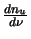 )
multiplied by the probability of a molecule spontaneously changing from the upper
to the lower level (ie. the Einstein A coefficient - A
)
multiplied by the probability of a molecule spontaneously changing from the upper
to the lower level (ie. the Einstein A coefficient - A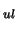 )
divided by
)
divided by 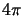 steradians. All this together
yields
steradians. All this together
yields
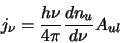 |
(2.23) |
which is the energy density emitted at a particular frequency in all directions per unit volume per second.
Similarly an absorption coefficient can be defined as
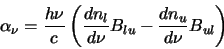 |
(2.24) |
Note that here stimulated emission is taken to be negative absorption. This is the amount of energy absorbed
per unit volume per second.





Next: Temperature Definitions
Up: The Theory Of Spectral
Previous: The Theory Of Spectral
1999-04-12
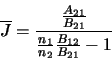
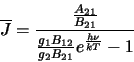
![]() )
multiplied by a function that measures the rate of change of the upper level population with frequency
(
)
multiplied by a function that measures the rate of change of the upper level population with frequency
(
![]() )
multiplied by the probability of a molecule spontaneously changing from the upper
to the lower level (ie. the Einstein A coefficient - A
)
multiplied by the probability of a molecule spontaneously changing from the upper
to the lower level (ie. the Einstein A coefficient - A![]() )
divided by
)
divided by ![]() steradians. All this together
yields
steradians. All this together
yields