




Next: A Generalised 2-D Radiative
Up: The STENHOLM Method
Previous: The STENHOLM Method
Solving the Radiative Transfer Equation Along a Line of Sight
Although there is no analytical solution to equation 3.13 when 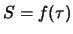 it is possible to
have a computer solve the equation by splitting the integral up into sections
it is possible to
have a computer solve the equation by splitting the integral up into sections
![\begin{displaymath}
I_{\nu_0}=\sum^n_{i=1} \left[ \int^{\tau_{\nu,i}}_{\tau_{\nu,i-1}} S_{\nu,i}(\tau)e^{-\tau_{\nu,i}}
d(\tau'_{\nu}) \right]
\end{displaymath}](img363.gif) |
(3.14) |
Where 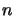 is chosen to be sufficiently large such that over the regions
is chosen to be sufficiently large such that over the regions
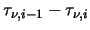 the
value of
the
value of
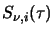 is effectively constant. If this condition holds then it is possible to integrate
to give
is effectively constant. If this condition holds then it is possible to integrate
to give
where
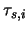 is the optical depth of segment
is the optical depth of segment 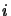 which should also satisfy
which should also satisfy
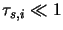 .
This is now in a format that a computer program can easily handle.
.
This is now in a format that a computer program can easily handle.
This then is the radiation intensity from one line of sight. In order to calculate the total radiation flux
falling on each geometry segment it is necessary to find the average intensity from many lines of sight in
many directions. Since the flux will be dependent on frequency it will be necessary to find the flux at
several different frequencies and then integrate over frequency to find the total flux.
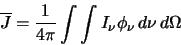 |
(3.16) |
Equation 3.16 shows the integral that performs this. 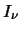 is the intensity from one line of
sight at a particular frequency as given in
equation 3.15 (the 0 has been dropped for convenience).
is the intensity from one line of
sight at a particular frequency as given in
equation 3.15 (the 0 has been dropped for convenience). 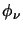 is the function that describes the line
profile and for a Gaussian profile is given by
is the function that describes the line
profile and for a Gaussian profile is given by
This can then be substituted back into equation 3.16 which can be integrated in
segments in an analogous manner to equation 3.15 to give
![\begin{displaymath}
\overline{J}=\frac{1}{4\pi}\sum_{d=1}^n\left[\sum_{s=1}^m\le...
...a e^{-\frac{\nu_s^2}{\nu_0^2}}\right)\Delta s \right] \Delta d
\end{displaymath}](img376.gif) |
(3.17) |
where 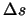 is the velocity step,
is the velocity step, 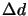 is the solid angle step size,
is the solid angle step size, 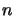 is the number of lines of sight (counted by
is the number of lines of sight (counted by
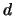 )
and
)
and 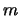 is the number of velocity steps across the line profile (counted by
is the number of velocity steps across the line profile (counted by 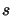 ). The solid angle step size is dependent
on the number of lines of sight and is simply
). The solid angle step size is dependent
on the number of lines of sight and is simply
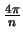 .
The line profile function is defined to be normalised
so that
.
The line profile function is defined to be normalised
so that
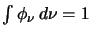 .
From this it can be deduced that
.
From this it can be deduced that
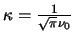 (this is shown in more detail for a similar calculation next to figure 4.13 on
page
(this is shown in more detail for a similar calculation next to figure 4.13 on
page ![[*]](icons/cross_ref_motif.gif) ). Substituting these into equation 3.17 enables
). Substituting these into equation 3.17 enables
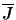 to be written as
to be written as
![\begin{displaymath}
\overline{J}=\frac{\Delta s}{n\sqrt{\pi}\nu_0}\sum_{d=1}^n\l...
...\nu,s} \index{flux}
e^{-\frac{\nu_s^2}{\nu_0^2}}\right)\right]
\end{displaymath}](img383.gif) |
(3.18) |
This is the total flux on a particular geometry segment due to the rest of the cloud. This is the information
that the statistical equilibrium equations need in order to be able to find the equilibrium population levels
that would be caused by such a radiation field.





Next: A Generalised 2-D Radiative
Up: The STENHOLM Method
Previous: The STENHOLM Method
1999-04-12
![\begin{displaymath}
I_{\nu_0}=\sum^n_{i=1} \left[ \int^{\tau_{\nu,i}}_{\tau_{\nu,i-1}} S_{\nu,i}(\tau)e^{-\tau_{\nu,i}}
d(\tau'_{\nu}) \right]
\end{displaymath}](img363.gif)