Thus far there are only a few examples of protostars known that exhibit features that could be caused by rotating
disks. The main reason for this is that the disks tend to be quite small (100s-1000s of AUs) and hence are at
the very limit of what present day telescopes can observe. However, there are several new telescope projects
in progress at present that should deliver dramatically higher resolutions and sensitivities in the first decade
of the 21![]() century. It will therefore be instructive to simulate what features telescopes of differing
resolutions can distinguish.
century. It will therefore be instructive to simulate what features telescopes of differing
resolutions can distinguish.
To do this consider a cloud that has the same envelope structure as that used for the testing of Buckley's
model [7] in section 5.2.3. To recap, this was a 0.047 pc radius cloud with the
inner 0.0175 pc collapsing primarily with a
![]() velocity profile but with an additional
velocity profile but with an additional
![]() profile adding to the velocity in the outer collapse regions. The molecular hydrogen distribution
follows a
profile adding to the velocity in the outer collapse regions. The molecular hydrogen distribution
follows a
![]() profile in the inner cloud, increasing to
profile in the inner cloud, increasing to ![]() in the outer cloud. Temperature follows
in the outer cloud. Temperature follows
![]() and the turbulent velocity and molecular abundance are constant throughout the cloud.
and the turbulent velocity and molecular abundance are constant throughout the cloud.
A disk is now placed in the centre of the cloud by making a disk shaped segment rotate with a Keplerian
velocity distribution - ie.
![]() where
where ![]() is the distance from the axis of symmetry in the cloud.
Initially there will be no additional density enhancement in this disk (ie. the parameters in the disk are exactly those
that the non-rotating cloud has except for the addition of rotation). The Keplerian velocity is defined by
is the distance from the axis of symmetry in the cloud.
Initially there will be no additional density enhancement in this disk (ie. the parameters in the disk are exactly those
that the non-rotating cloud has except for the addition of rotation). The Keplerian velocity is defined by
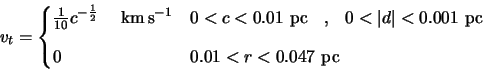
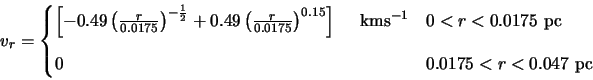
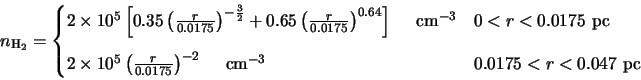
![\includegraphics[scale=1.]{cenbeam1.eps}](img1166.gif)
![\includegraphics[scale=1.]{cenbeam2.eps}](img1167.gif) |
This can be seen in figure 6.5 where a pencil beam is used on two
clouds, one with the rotation velocity capped at 8 km s![]() and the other with the velocity increasing up to the
innermost shell at
and the other with the velocity increasing up to the
innermost shell at
![]() pc where the velocity peaks at 32 km s
pc where the velocity peaks at 32 km s![]() .
The line profiles are shown
for offsets of 0
.
The line profiles are shown
for offsets of 0
![]() ,
0.2
,
0.2
![]() ,
0.3
,
0.3
![]() ,
0.5
,
0.5
![]() & 1
& 1
![]() .
Note that at a distance of 140pc
.
Note that at a distance of 140pc
![]() pc
pc![]() AU and that
the 8 km s
AU and that
the 8 km s![]() mark is reached at approximately 0.00015 pc so it might be expected that only the two line
profiles that are at 0.1
mark is reached at approximately 0.00015 pc so it might be expected that only the two line
profiles that are at 0.1
![]() and 0.2
and 0.2
![]() will show any significant differences and this is indeed the case. The lack
of smoothness in these two line profiles is due to there being insufficient rings in the inner cloud leading to
large differences in velocities from one ring to the next causing the step like effect. It can be seen that
only line profiles very close to the centre of the cloud are affected by the cut off. In any realistically sized
beam this problem is likely to be smeared out. It therefore seems valid to cap the velocity at 8 km s
will show any significant differences and this is indeed the case. The lack
of smoothness in these two line profiles is due to there being insufficient rings in the inner cloud leading to
large differences in velocities from one ring to the next causing the step like effect. It can be seen that
only line profiles very close to the centre of the cloud are affected by the cut off. In any realistically sized
beam this problem is likely to be smeared out. It therefore seems valid to cap the velocity at 8 km s![]() .
This rules out the possibility of unpredictable behaviour caused by using only 11 velocity steps to cover a
velocity range of 30+ km s
.
This rules out the possibility of unpredictable behaviour caused by using only 11 velocity steps to cover a
velocity range of 30+ km s![]() in the lambda iteration routine.
in the lambda iteration routine.
The general shape of the line profiles are as might be expected for the cloud with a significant line wing due to the rotation and a large self absorption dip at zero velocity caused by the cooler, stationary outer half of the cloud. The extra small dips and asymmetries, especially significant on the line profile that looked at the centre of the cloud, are due to the cloud being fairly optically thick which causes additional self absorption besides that caused by the outer regions of the cloud.
![\includegraphics[scale=1]{rotbeam2.eps}](img1171.gif)
![\includegraphics[scale=1]{rotbeam1.eps}](img1172.gif) Line profiles for a 15
Line profiles for a 15
| nodd | no. of points | |
| solid | 201 | 40401 |
| dashed | 101 | 10201 |
| dot-dashed | 51 | 2601 |
| dotted | 21 | 441 |
| dot-dot-dot-dash | 11 | 121 |
| nodd | run time (min) |
| 11 | 0.15 |
| 21 | 0.37 |
| 51 | 1.9 |
| 101 | 7.4 |
| 201 | 29.2 |
![\includegraphics[scale=1]{colcoefcheck1.eps}](img1174.gif)
![\includegraphics[scale=1]{colcoefcheck2.eps}](img1175.gif) Position velocity diagram for HCO+ 4
Position velocity diagram for HCO+ 4
Clearly it would be desirable to keep nodd to around 50 if possible and for all beams that do not cover the
centre of the cloud around
![]() would be adequate. A useful future modification to the program
would be one that enables it to automatically select the best value of nodd depending on where in the
cloud the beam is located. This would enable maps of the cloud to be produced much faster than at present. For
now however, it is necessary to choose the value of nodd that is needed at the cloud centre and use it
for all positions on the cloud. The values that will generally be used in the following models are either
would be adequate. A useful future modification to the program
would be one that enables it to automatically select the best value of nodd depending on where in the
cloud the beam is located. This would enable maps of the cloud to be produced much faster than at present. For
now however, it is necessary to choose the value of nodd that is needed at the cloud centre and use it
for all positions on the cloud. The values that will generally be used in the following models are either
![]() or
or ![]() .
A model producing line profiles at 50 positions across the cloud takes a little less
than 1 hour for
.
A model producing line profiles at 50 positions across the cloud takes a little less
than 1 hour for ![]() but around 3 hours for
but around 3 hours for ![]() .
The time taken to produce a position velocity
diagram depends not only on the number of grid points used to model the beam (and of course the number of rings
in the cloud) but also the optical depth of the cloud. Calculating line profiles for an optically thick cloud
can take much longer than for an optically thin cloud since each line of sight will then be split into many
subsections when solving the radiative transfer equation (see page
.
The time taken to produce a position velocity
diagram depends not only on the number of grid points used to model the beam (and of course the number of rings
in the cloud) but also the optical depth of the cloud. Calculating line profiles for an optically thick cloud
can take much longer than for an optically thin cloud since each line of sight will then be split into many
subsections when solving the radiative transfer equation (see page ![]() ).
).
A final problem that needs investigating are the collision coefficients. For HCO+ there are two sources of these
collision rates. Either the rates of N![]() H
H![]() as calculated by Sheldon Green [10] are used and
multiplied by 2.5 as suggested by Monteiro [22] to simulate HCO
as calculated by Sheldon Green [10] are used and
multiplied by 2.5 as suggested by Monteiro [22] to simulate HCO![]() or the rates from T.S. Monteiro
(private communication but based on work published in [22]) can be
used. The former cover the correct temperature range for this kind of cloud, ie. 5-40 K but only cover
the first 6 levels. The later cover the first 10 levels but unfortunately the temperature range is 20-250 K. The
temperature range in this model cloud is 8.8-35 K so the outer parts of the cloud are well below the
lower end of the range for which collision coefficients are given. Nonetheless when attempting to model high-J
transitions there is no choice other than to use these coefficients. The problem is probably not too severe for
two reasons. Firstly the high-J transitions will map mainly the hot parts of the cloud which in this case means
only the central core and here the temperatures are close to or above 20 K. Also the collision coefficients
do not change much with temperature. Therefore the interpolation routine which uses the collision coefficients
at the lowest two temperatures
to linearly extrapolate below the lowest available temperature will work fairly well if there are no dramatic
changes between 20 K and 8 K (which there are not for most levels as can be seen from the S. Green
rates). A check on this can be performed by comparing output from a model at J=
or the rates from T.S. Monteiro
(private communication but based on work published in [22]) can be
used. The former cover the correct temperature range for this kind of cloud, ie. 5-40 K but only cover
the first 6 levels. The later cover the first 10 levels but unfortunately the temperature range is 20-250 K. The
temperature range in this model cloud is 8.8-35 K so the outer parts of the cloud are well below the
lower end of the range for which collision coefficients are given. Nonetheless when attempting to model high-J
transitions there is no choice other than to use these coefficients. The problem is probably not too severe for
two reasons. Firstly the high-J transitions will map mainly the hot parts of the cloud which in this case means
only the central core and here the temperatures are close to or above 20 K. Also the collision coefficients
do not change much with temperature. Therefore the interpolation routine which uses the collision coefficients
at the lowest two temperatures
to linearly extrapolate below the lowest available temperature will work fairly well if there are no dramatic
changes between 20 K and 8 K (which there are not for most levels as can be seen from the S. Green
rates). A check on this can be performed by comparing output from a model at J=
![]() using both sets
of collision rates. This is shown in figure 6.7. It can clearly
be seen that for all practical purposes these figures are the same and it is therefore possible to proceed with
confidence to use only the collision coefficients that extend up to J
using both sets
of collision rates. This is shown in figure 6.7. It can clearly
be seen that for all practical purposes these figures are the same and it is therefore possible to proceed with
confidence to use only the collision coefficients that extend up to J![]() .
.