




Next: A Detailed Comparison with
Up: Testing by Comparison with
Previous: The optically thick LTE
The LVG case
The Large Velocity Gradient (LVG) case (see section 3.2) shows that for a spherical infalling cloud the observed antenna temperature
depends only on 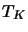 ,
,
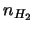 and
and
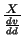 (ie. the kinetic temperature, the
hydrogen abundance and the relative abundance divided by the rate of change of velocity along the
line of sight, respectively).
(ie. the kinetic temperature, the
hydrogen abundance and the relative abundance divided by the rate of change of velocity along the
line of sight, respectively).
Theoretical output for a LVG model
[l]
![\includegraphics[scale=0.5]{lvg2.eps}](img1041.gif) If these parameters are all chosen to be constant throughout the
cloud then the antenna temperature will be constant over its entire velocity range and will
produce a line shape as shown in figure 5.10. The line will be flat toppped and will extend from
If these parameters are all chosen to be constant throughout the
cloud then the antenna temperature will be constant over its entire velocity range and will
produce a line shape as shown in figure 5.10. The line will be flat toppped and will extend from
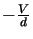 to
to
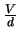 where
where 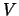 is the infall velocity of the outer edge of the cloud and
is the infall velocity of the outer edge of the cloud and 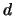 is
dependent on the distance from the cloud centre that the line of sight takes as shown in
figure 5.11.
is
dependent on the distance from the cloud centre that the line of sight takes as shown in
figure 5.11.
Line of sight direction
[r]
![\includegraphics[scale=0.5]{lvg.eps}](img1044.gif) Setting
Setting 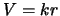 where
where 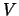 is the infall
velocity,
is the infall
velocity, 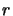 is the radius and
is the radius and 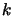 is a constant it is then clear from figure 5.11 that
is a constant it is then clear from figure 5.11 that
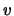 ,
the velocity component along any given line of sight is given by
,
the velocity component along any given line of sight is given by
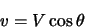 |
(5.5) |
where 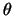 is the
angle between the line of sight and the line drawn from the centre of the cloud to the point where the line of
sight exits the cloud as shown in figure 5.11. Also simple
geometry gives
is the
angle between the line of sight and the line drawn from the centre of the cloud to the point where the line of
sight exits the cloud as shown in figure 5.11. Also simple
geometry gives
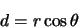 |
(5.6) |
Dividing equation 5.5 by equation 5.6 then yields
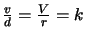 and thus
and thus
which, as required, is constant. In other
words, with these conditions, the emission along the line of sight is evenly spread over the
velocity range present along the line of sight. This velocity range has its extremes at the entry
and exit points of the line of sight from the cloud which are given by
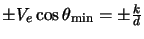 where
where 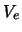 is the velocity at the exit point which is
is the velocity at the exit point which is 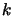 if the
radius is normalised and
if the
radius is normalised and
 is the value of
is the value of 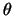 at the exit point which gives
at the exit point which gives
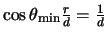 for a normalised
for a normalised 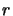 .
.
![\includegraphics[scale=1]{lvgeg.eps}](img1054.gif) LVG example output
LVG example output
Figure 5.12 shows the output for a model with 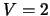 kms
kms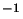 .
Output is shown at four positions
which correspond to the centre of the cloud, half way to the edge of the cloud,
.
Output is shown at four positions
which correspond to the centre of the cloud, half way to the edge of the cloud,
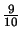 of the way
to the edge of the cloud and
of the way
to the edge of the cloud and
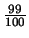 of the way
to the edge of the cloud respectively (from left to right). It can be seen the the output is as predicted in
figure 5.10 with the line always reaching the same maximum temperature but with a decreasing line
width as the telescope looks closer to the edge of the cloud.
of the way
to the edge of the cloud respectively (from left to right). It can be seen the the output is as predicted in
figure 5.10 with the line always reaching the same maximum temperature but with a decreasing line
width as the telescope looks closer to the edge of the cloud.





Next: A Detailed Comparison with
Up: Testing by Comparison with
Previous: The optically thick LTE
1999-04-12
![\includegraphics[scale=0.5]{lvg2.eps}](img1041.gif) If these parameters are all chosen to be constant throughout the
cloud then the antenna temperature will be constant over its entire velocity range and will
produce a line shape as shown in figure 5.10. The line will be flat toppped and will extend from
If these parameters are all chosen to be constant throughout the
cloud then the antenna temperature will be constant over its entire velocity range and will
produce a line shape as shown in figure 5.10. The line will be flat toppped and will extend from
![\includegraphics[scale=0.5]{lvg.eps}](img1044.gif) Setting
Setting ![\includegraphics[scale=1]{lvgeg.eps}](img1054.gif)