




Next: The LVG case
Up: Testing by Comparison with
Previous: Testing by Comparison with
The optically thick LTE case
It has been shown earlier (equation 3.6) that the radiation intensity at a frequency
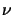 observed by a telescope is given by
observed by a telescope is given by
![\begin{displaymath}
I_{\rm obs}=\left[ I_{T_{\rm EX}} - I_{T_{B}} \right] \left( 1-e^{-\tau}\right)
\end{displaymath}](img1026.gif) |
(5.1) |
where 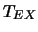 is the excitation temperature in the cloud (which is assumed to be constant) and
is the excitation temperature in the cloud (which is assumed to be constant) and 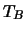 is the cosmic
background radiation temperature (note that
is the cosmic
background radiation temperature (note that
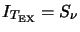 ). For a black body
). For a black body
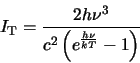 |
(5.2) |
In the Rayleigh-Jeans limit (
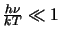 )
)
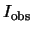 can be written
can be written
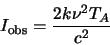 |
(5.3) |
Note that this is the definition of 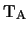 ,
in other words the antenna temperature is defined as being the
temperature that would be caused by a blackbody radiating in the Rayleigh-Jeans limit.
The radiation from the cloud and cosmic background, however, are not
necessarily in the Rayleigh Jeans limit and thus are described by equation 5.2. Substituting these
into equation 5.1 and cancelling where appropriate yields
,
in other words the antenna temperature is defined as being the
temperature that would be caused by a blackbody radiating in the Rayleigh-Jeans limit.
The radiation from the cloud and cosmic background, however, are not
necessarily in the Rayleigh Jeans limit and thus are described by equation 5.2. Substituting these
into equation 5.1 and cancelling where appropriate yields
![\begin{displaymath}
T_A=\frac{h\nu}{k}\left[\frac{1}{e^{\frac{h\nu}{kT_{EX}}}-1}-\frac{1}{e^{\frac{h\nu}{kT_{B}}}-1}\right]\times(1-e^{-\tau})
\end{displaymath}](img1034.gif) |
(5.4) |
If the collision rate between molecules in the cloud is very high then the excitation temperature will be
approximately equal to the kinetic temperature. Thus by setting the excitation temperature in the cloud to a
given value (say 20 K), insuring the collision rate is very high (this is done by setting the
hydrogen density to a very high level) and choosing the molecular abundance such that
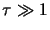 in the line
centre the precise value of the line peak can be calculated. For
in the line
centre the precise value of the line peak can be calculated. For  CO the
temperatures should be
CO the
temperatures should be
| Transition |
Temperature (K) |
3
 2
2 |
13.058 |
2
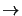 1
1 |
14.952 |
1
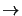 0
0 |
16.582 |
Line profiles with
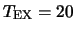 K,
K,
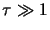 in the line centre for J
in the line centre for J
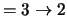 (left),
J
(left),
J
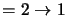 (middle) and J
(middle) and J
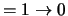 (right).
(right).
The figures above demonstrate that the program successfully reproduces the lines at the temperatures
predicted. The flat topped line shape is also as might be expected since the height of the top represents the
temperature that will be caused by the emission from molecules at a particular velocity that have their
excitation temperature equal to the kinetic temperature of the gas. The width of the line is determined by the
random motion of the molecules in the gas. The velocity distribution of this motion is Gaussian and therefore
further away from the line centre there will be fewer molecules at a particular velocity. As long as there are
sufficient molecules so that
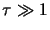 the emission temperature will still be at the value
given by equation 5.4, this causes the flat top. However, once the columnn density drops below the required
level the emission temperature drops off. In the above figures the density has been set so high that the
optical depth only becomes less than one at the very edges of the lines.
the emission temperature will still be at the value
given by equation 5.4, this causes the flat top. However, once the columnn density drops below the required
level the emission temperature drops off. In the above figures the density has been set so high that the
optical depth only becomes less than one at the very edges of the lines.





Next: The LVG case
Up: Testing by Comparison with
Previous: Testing by Comparison with
1999-04-12
![\includegraphics[scale=0.9]{line1.eps}](img1035.gif)
![\includegraphics[scale=0.9]{line2.eps}](img1036.gif)
![\includegraphics[scale=0.9]{line3.eps}](img1037.gif)
![]() the emission temperature will still be at the value
given by equation 5.4, this causes the flat top. However, once the columnn density drops below the required
level the emission temperature drops off. In the above figures the density has been set so high that the
optical depth only becomes less than one at the very edges of the lines.
the emission temperature will still be at the value
given by equation 5.4, this causes the flat top. However, once the columnn density drops below the required
level the emission temperature drops off. In the above figures the density has been set so high that the
optical depth only becomes less than one at the very edges of the lines.