Re-labelling the Data Arrays

Hereafter the program proceeds much as described in Matthews [20] with the exception of the matrix inversion routine which is as in section 4.7.4 and the output which is as described in section 4.9. The main difference over the original version is the labelling of the levels. As mentioned previously linear molecules only undergo transitions that go from level J to level J-1 which enables a program to deal with all transitions using just a simple loop with only one counter. So for CO for example the counter will run from 1 to 11 (the number of levels for which collision coefficients are available). 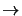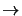It is then easy to have several one dimensional arrays for the frequency information, Einstein A & B coefficients and other required data where the first array position is for transition J=1 $\rightarrow$0, the second position is for transition J=2 $\rightarrow$1 and so on. This system breaks down when the simple selection rules for linear molecules no longer apply. However, there is a way around this which still retains the original structure of the program. If two one dimensional arrays are defined (tri and trj in the program) with the first storing the upper J level number of a transition and the other storing the lower J level of a transition then the original program structure can still be used. Consider for example a 4 level molecule with has only the transitions $1 \rightarrow 0$, $3\rightarrow1$, $4\rightarrow2$. 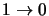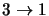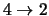Then the arrays would be filled:

Element number	tri	trj
1	1	0
2	3	1
3	4	2

Now every transition is assigned a label from1 up to the number of transitions present. The arrays containing the frequency of the transitions and the Einstein coefficients are now made 2 dimensional and are filled where appropriate (ie. for all allowed transitions). The program can then loop through all transitions using just the one counter and will refer to a specific transition using the 2 decoding arrays described above. eg. to get the Einstein coefficients for the second transition above the program would call 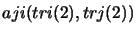$aji(tri(2),trj(2))$(where aji stores the Einstein A coefficients).

This modification enables the program to run for any molecule as long as the appropriate data is available in the input files. For linear molecules the linefreq.f program mentioned above (page ) will calculate the necessary input files. For other more complex molecules the files will have to be created using an appropriate method which will depend on the source of the parameters.