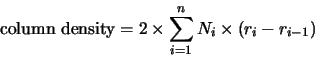



Next: Re-labelling the Data Arrays
Up: Generalising the STENHOLM program
Previous: Source of the Einstein
Setting up the model cloud
The program starts by reading in all the required data for the cloud to be modelled from the various files.
Once this is done it proceeds to construct the
model cloud and calculate the parameters necessary for the radiative transfer
modelling.
First the sizes of the shells throughout the cloud are calculated using
where
 is the cloud radius,
is the cloud radius,
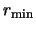 is the radius of the
innermost shell and
is the radius of the
innermost shell and 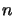 is the number of shells.
is the number of shells.
Next the physical parameters in each shell are worked out (according to the parameters provided
in the input files). Once these are known the collision coefficients for each transition
can be worked out in each shell. This uses simple linear interpolation of the figures
provided for various temperatures in the COEFDATA.DAT file. At present the program can
only interpolate for temperatures that lie between the smallest and largest
temperatures for which collision coefficients are provided.
The column density is calculated simply by adding up the individual segments in each
shell. Each shell's column density is easily calculated as the density and thickness
of the shell is known. The figure returned is
where 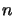 is the number of shells,
is the number of shells, 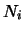 is the molecular density in the
is the molecular density in the
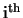 shell and
shell and 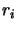 is the outer radius of the
is the outer radius of the
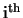 shell (with
shell (with 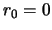 ).
Note that this is the column density right through the cloud (ie. not just to the
centre).
).
Note that this is the column density right through the cloud (ie. not just to the
centre).




Next: Re-labelling the Data Arrays
Up: Generalising the STENHOLM program
Previous: Source of the Einstein
1999-04-12
![\begin{displaymath}r_{i+1}=r_{\rm min}\left[\left(\frac{r_{\rm cloud}}{r_{\rm min}}\right)^
{\frac{1}{n-1}}\right]^i
\hspace*{6em} i=0,\ldots,n-1\end{displaymath}](img413.gif)
![\begin{displaymath}r_{i+1}=r_{\rm min}\left[\left(\frac{r_{\rm cloud}}{r_{\rm min}}\right)^
{\frac{1}{n-1}}\right]^i
\hspace*{6em} i=0,\ldots,n-1\end{displaymath}](img413.gif)