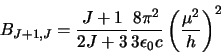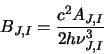Next: Setting up the model
Up: Generalising the STENHOLM program
Previous: New features
Source of the Einstein Coefficients
For linear molecules a simple formula can be used to calculate all the needed input data
for the modelling and this was done within the original version of the program. Since this is not possible for some of the more complex
molecules the program is now fed a group of files containing the Einstein coefficients and other parameters for
the molecule to be modelled. An extra program has been provided which given some initial data will
calculate the required values and place them in the correct files. linefreq.f needs to be told the name of the molecule
for which a file is required, the highest level for which output is required (this
will usually be the highest level for which collision coefficients are available), the dipole
moment, 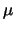 and the rotation constant,
and the rotation constant, 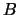 .
Note that the rotation constant must be
entered in Hertz (ie. not MHz or GHz). From these data linfreq.f then calculates the
frequency,
.
Note that the rotation constant must be
entered in Hertz (ie. not MHz or GHz). From these data linfreq.f then calculates the
frequency,
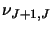 for all transitions
for all transitions
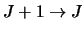 as well as the Einstein coefficients
as well as the Einstein coefficients
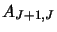 and
and 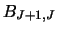 .
To do this it uses:
.
To do this it uses:
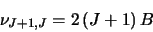 |
(4.1) |
Where equation 4.3 simply substitutes equation 4.1 in for
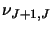 in
equation 4.2.
in
equation 4.2.
Finally, it also returns the value of 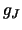 ,
the degeneracy, which is given by:
,
the degeneracy, which is given by:
For non linear molecules it is a non-trivial task to calculate any of these values and
it is therefore preferable to use data that has already been calculated. In the case of
formaldehyde this data is taken from [15]. The program freqsortc.f takes the
Einstein A coefficients and the frequencies for each transition as given in the input
files h2co_acoefs_ortho.txt and h2co_acoefs_para.txt. These files are scanned in
versions of the tables given in Kegel [15] and present the data in rows, where
each row represents one transition in the format:
The format used here for labelling the different levels is slightly different to the
usual 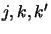 and is also different to the labelling system used in the collision
coefficients file, which uses a
and is also different to the labelling system used in the collision
coefficients file, which uses a 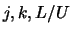 system where
system where 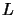 stands for lower and
stands for lower and 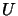 for
upper. In terms of the usual
for
upper. In terms of the usual 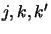 system
system 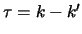 and
and 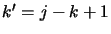 for a Lower
transition and
for a Lower
transition and 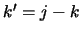 for an upper transition. Using these data and also the energy
of each level, taken from ortho.txt and para.txt the program calculates the Einstein B
coefficient using the equation of detailed balance:
for an upper transition. Using these data and also the energy
of each level, taken from ortho.txt and para.txt the program calculates the Einstein B
coefficient using the equation of detailed balance:
(this is simply equation 2.24 re-arranged). Where necessary the main
STEN program then calculates 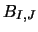 from:
from:
As before 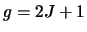 .
The
energy data (which is used to calculate
.
The
energy data (which is used to calculate 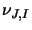 by the use of
by the use of
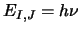 where
where
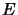 is the energy difference between two levels) is multiplied by
is the energy difference between two levels) is multiplied by
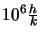 (
(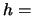 Planck's constant,
Planck's constant, 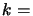 Boltzmann's
constant) in order to change the units from those given in the input file to those
required by the STEN program. It is also worth noting that the ortho.txt and para.txt
files include a list of numbers in the first column that give each level a label
running from one to however many levels there happen to be. These numbers are the
level numbers that the main STEN program refers to. The data on the
Boltzmann's
constant) in order to change the units from those given in the input file to those
required by the STEN program. It is also worth noting that the ortho.txt and para.txt
files include a list of numbers in the first column that give each level a label
running from one to however many levels there happen to be. These numbers are the
level numbers that the main STEN program refers to. The data on the 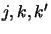 values is
never passed to the main program which also relies on the input file FREQ.*** to know
how many transitions are possible and which level numbers the transitions link. This
information is also calculated by the freqsortc.f program which considers all possible
transitions in the range for which there are data. It then rules out all forbidden
transitions and all those which are absorption transitions. All the remaining
possibilities should then have data available in the h2co_acoefs_ortho.txt (or the
para equivalent) file. These data are then written into the FREQ.*** file.
values is
never passed to the main program which also relies on the input file FREQ.*** to know
how many transitions are possible and which level numbers the transitions link. This
information is also calculated by the freqsortc.f program which considers all possible
transitions in the range for which there are data. It then rules out all forbidden
transitions and all those which are absorption transitions. All the remaining
possibilities should then have data available in the h2co_acoefs_ortho.txt (or the
para equivalent) file. These data are then written into the FREQ.*** file.





Next: Setting up the model
Up: Generalising the STENHOLM program
Previous: New features
1999-04-12