An oblate model

Since the prolate model suffers from significant problems that cannot be solved with a realistic model it seems that an oblate model is a more appropriate choice of cloud shape. This could be viewed as being a disk like structure with its axis of symmetry aligned in a NE-SW direction. This disk can be allowed to rotate about this axis of symmetry which will have the effect of shifting the spectra in the NW and SE corners of the grid as required. This is now a much more physically realistic model. The rotation has to be solid body rotation as the velocity shift is larger further from the centre (the opposite applies to Keplerian rotation). However, this cloud is likely to be magnetically supported (see Williams [35]) which would also have the effect of allowing solid body rotation since the magnetic field would hold the entire cloud together as though it were solid. This would only apply for low velocities but the velocities here are only a few 100 m s$^{-1}$ so this too is a reasonable assumption. Figure 7.5 shows the results from such a model. The model cloud was taken to be 0.1pc in radius and 0.05pc in height. The parameters for the best fit model were distributed according to

$$n_{\rm H_2}={\rm min} \left(250000,600000 \times \frac{r}{0.001}^{-0.95-0.35 \left\vert \sin \theta \right\vert} \right)$$

$$T_k=12$$

$$V_{\rm turb}=0.20-0.20\frac{r}{0.01}$$

$$V_{\rm in}=-0.12\frac{r}{0.1}$$

$$V_{\rm rot}=0.35\frac{r_c}{0.1}$$

$$X_{N_2H^+}=1\times10^{-9}$$

$r$ is the distance in parsecs from the cloud centre and $r_{c}$ is the distance, also in parsecs, along the minor axis of the cloud (ie. in the plane of the disk). The cloud was rotated 35$^\circ$ in the plane of the sky as suggested by Williams et al. [35] but no tilt was included - ie. it is assumed that the disk is being viewed edge on.

  

Figure: Grid spectra of L1544 in N$_2$H$^+$ $1 \rightarrow 0$. The offsets are from $\alpha (2000)=5^{\rm h}04^{\rm m}16^{\rm s}.6$ , $\delta(2000)=25^\circ11^\prime7^{\prime \prime}.8$. The blue histogram line is data from Williams et el. [35] and the red line is the modelled result.

Note that the H$_2$ distribution was 'anchored' at close to the centre of the cloud (0.001pc) rather than at the outer cloud edge. This means that the value of $c$ as given in equation 7.1 is the actual density at 0.0001pc after which the value drops at a rate defined by the power law chosen. Previously the value of $c$ represented the density at the outer edge and the density then rose as defined by the power law chosen. This new system has the advantage that the size of the cloud can be varied without altering the distribution of H$_2$ in the inner part of the cloud. In addition the density was capped at a value of 250000 to prevent infinite values at the cloud centre. For this cloud with dimensions of 0.1$\times$0.05pc this means that the outer edge of the cloud still has a density of around 7500 cm$^{-3}$ implying a very abrupt edge to the cloud. This may not be as unrealistic as it seems as there has been evidence presented by Bacmann et al. [4] that clouds such as this one do indeed have a very steep gradient at their outer edge. They suggest that this '...sharp edge [occurs] at $R \sim 15000 - 30000$ AU [0.07-0.15pc] and appear[s] to be decoupled from the parent cloud'. This is exactly the range that appears to give the best fit here.

The density profile is also significantly flatter than the usual value of $r^{-2}$ used in the Shu 'standard' model [29]. Using a value of $r^{-2}$ causes the emission to drop to virtually zero well before the observed edge of the cloud (or alternatively if the emission is forced to be correct at the cloud edge it is then far too bright at the cloud centre). However, there has been an increasing amount of evidence in recent years that the $r^{-2}$ density profile is not correct (see for example [34,2]) and that a less steep profile is more appropriate. This is borne out by these results as the two density profiles used were $r^{-0.95}$ and $r^{-1.3}$ (along the major and minor axes of the cloud respectively). There is some flexibility as to the density profile chosen as minor changes (ie. $-0.95 \pm 0.15$ say) can be accommodated by changing other parameters. As an interesting exercise an attempt was made to model the cloud with a linear profile

$$n_{\rm H_2}=70000-63000 \times \frac{r_c}{0.047}-\left\vert(63000 \times \sin(\theta)\frac{r_d}{0.04}\right\vert$$

  

Figure: Grid spectra of L1544 in N$_2$H$^+$ $1 \rightarrow 0$. The origin is as in figure 7.5. The blue histogram line is data from Williams et al. [35] and the red line is the modelled result for a cloud with a linear H$_2$distribution profile.

Although this fit is clearly not as good for such a simple model it is remarkably good. The intensity is overestimated for rings around the centre of the cloud but in certain directions the errors are quite small. Consider the line from the centre of the cloud and running to the NW - here the differences are no more than 10-20%. A significantly better fit could no doubt be obtained with a 2 component linear fit. However, since the power law distribution obviously fits better the linear distribution will not be pursued further here.

A Gaussian distribution was also tried but it was not possible to find a good solution for this and for this object at least a Gaussian distribution seems inappropriate.

The turbulence was set to 0.2 km s$^{-1}$ at the centre of the cloud (the 0.22 km s$^{-1}$ used by Williams gave slightly too large line widths) but then allowed to decrease further out in the cloud, eventually dropping to virtually zero on the outer edge of the disk. Although zero turbulence is clearly unrealistic a small increase in the turbulence further out in the cloud has little effect on the results. Larger increases though tend to increase the size of the absorption dip that appears on the central spectra. This is because the central absorption dip is caused by the material in the outer part of the cloud. The effect of more turbulence in the outer cloud on the absorption dip can however be mitigated by applying a velocity gradient across the outer cloud material (see discussion below on the infall velocities). The reduced turbulence was also included to decrease the width of the spectra that appear in the NE and SW corners of the grid. The innermost spectra are however quite sensitive to the amount of turbulence: any less and the lines become too narrow, any more and they become too wide.

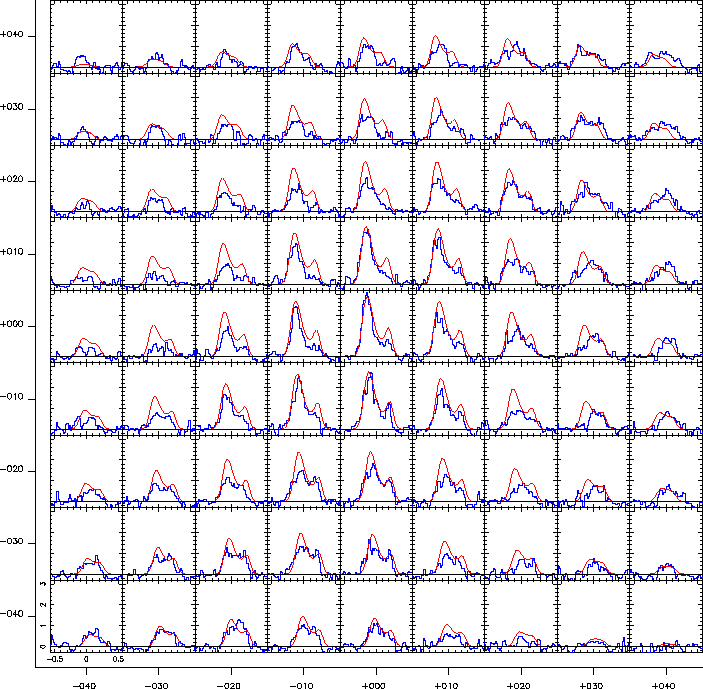
Probably the most interesting feature of this model cloud is the infall velocity gradient. This has been set to zero at the cloud centre and then increases linearly with radius to a maximum at the outer edge of the cloud. This is in direct contrast to the 'inside-out collapse' scenario envisaged by Shu [29]. It is, however, not possible to correctly fit the absorption dips correctly with either a constant infall gradient or a gradient that decreases with distance from the cloud centre. If the outer regions of the cloud are all moving at the same velocity then it is not possible to get the width of the line down to a sufficiently low level that the absorption dip fits the observed spectra as the dip is too wide and too deep. However, if the material is spread out in velocity, then the absorption will also be spread out over a wider velocity range and will therefore produce a weaker absorption dip. The size of the absorption dip can therefore be adjusted by varying the amount of velocity change in the cloud. This specifically affects the secondary peak on the central spectra. With zero infall velocity both peaks are the same height. Increasing the infall velocity gradually reduces the size of the secondary peak and increases the size of the primary peak (since the absorption dip is moved off one peak and over the top of the other). It is clear from the data that the cloud is not entirely symmetric which makes it impossible to reproduce precisely without a 3-D modelling program. It is therefore necessary to find a compromise solution - the one presented in figure 7.5 seems a reasonable compromise with the secondary peak being slightly too strong in the north and slightly too weak in the south. Contradicting this interpretation of faster infall in the outer cloud somewhat are the line shapes further away from the centre. These appear to be slightly double peaked but symmetrical which is usually a sign of no infall velocity (as would be expected for the Shu model in the outer cloud). However, a stationary cloud does not reproduce these shapes either as the absorption dip is quite strong even this far out. It is therefore presently an unsolved problem as to how to reproduce these line shapes. It seems unlikely that this is a noise artifact since it appears in numerous spectra. This problem seems to restrict itself to close to the plane of the disk since the spectra located well above and below the disk appear to be fit quite well again.

The rotation of the cloud as discussed previously has to be solid body rotation rather than Keplerian. If there is any central body rotating with a Keplerian velocity distribution then it must be very small as there is no evidence of such rotation on the spectra at the cloud centre where such an effect would be most easily noticed. The rotation has also been reduced outside the disk. The spectra in the NE corner of the grid suggest this reduction could have been more extreme but the spectra in the SW corner suggest the opposite so this again is a compromise caused by the program not being a full 3-D solution. More data further out may help clarify the situation since if the solid body rotation carries on to the outer edge of the cloud it will be here that the highest velocities are observed.

In summary, the model has been chosen to provide the best possible fit for the innermost few spectra with a reasonable fit further out. More work would probably improve the combined fit. The biggest discrepancy occurs in the NW corner. However, referring to figure 7.3 it can be seen that there is a secondary intensity peak in this corner of which no account has been taken. Therefore this discrepancy is not serious. The same can be said for the inaccurate spectra due south of the centre where an arm of stronger emission exists. These features cannot be modelled with a program that requires axial symmetry. It might be possible to get better fits by moving the cloud centre to the NW by about 10 $^{\prime \prime}$ and then placing a density enhancement torus around the centre to try and simulate the two density peaks. However, this cannot be a perfect solution since the torus would have to be symmetric and the two peaks are clearly not equal in size. Additionally it would be harder to find a physical justification for such a torus. More likely is possibly that two stars are forming in two separate clumps. With these provisos the modelled line profiles seem to be remarkably close to the observed spectra.

Telescope data from L1554 taken from Tafalla et al. [31].  [l] The N$_2$H$^+$ observations of L1544 presented by Williams et al. [35] are infact only a subset of a more extensive data set presented in Tafalla et al. [31]. In this they present observations in several isotopes of CO and CS as well as HCO$+$, H$_2$CO, C$_3$H$_2$ and 800$\mu$m continuum data. As these molecules all have different optical depths they can be used to probe the structure of the cloud better than if only one transition of one molecule is used. Although no attempt will be made here to produce an overall best fit model that takes into account all the different transitions they have published it is easy to simply output spectra for other molecules using the model developed from the N$_2$H$^+$ spectra. The only change to the model necessary is the relative abundance of each molecule. Figure 7.7 shows data for the $1 \rightarrow 0$ transitions of CO, $^{13}$CO and C$^{18}$O. The beam size used was 45.5 $^{\prime \prime}$, relatively large because the data were taken with the FCRAO 14m telescope. The dashed line for the CO data represents the uncertainty due to error beams caused by the FCRAO dish. The spectra for a dish with no error beams (ie. such as the 'perfect' dish used to model the cloud) would lie between the solid and the dashed line.

Model output for the $1 \rightarrow 0$ transition of CO (solid line), $^{13}$CO (dashed line) and C$^{18}$O (dot-dashed line).  [r] Figure 7.8 shows the same transitions but this time for the modelled data. The only changes made to the model were the relative abundance of the trace molecules. The values shown in table 6.1 were used for the abundances. It is immediately clear that the primary test has been successfully met in that the lines show no self absorption. Closer inspection shows also that the maximum intensities are very similar. Table 7.1 shows the peak intensities and line widths for the telescope data and the modelled results. The comparison is satisfactory considering no effort was made to fit these extra spectra during the modelling. In all cases the modelled result is slightly below the measured value (for the $^{12}$CO transition Tafalla et al. [31] believe the higher value is more likely to be correct) by approximately 10-20%. However, although the intensities are correct the line widths fall well short of the required width for the $^{12}$CO and $^{13}$CO transitions. Tafalla et al. performed limited Monte Carlo simulations of the cloud and suffered the same problems. It is probable that at least part of the problem is caused by the chosen turbulence in the cloud being reduced to zero at the outer edge of the cloud. This would make these lines significantly narrower than if the turbulence did not decrease with radius. Some support for this explanation is given by the better agreement for the C$^{18}$O line which probes deeper into the cloud and thereby sees material with a higher turbulence.

 

Table: Maximum intensities of telescope data and modelled results for CO isotopes. For the $^{12}$CO transition the two values are the range within which the peak may lie.

Isotope	Telescope data	Modelled result	Telescope data	Modelled result
	(K)	(K)	(FWHM - km s$^{-1}$)	(FWHM - km s$^{-1}$)
$^{12}$CO	8-13	9.0	1.1	0.65
$^{13}$CO	9	8.1	0.7	0.45
C$^{18}$O	4.7	4.0	0.4	0.3

   

Figure: FCRAO grid spectra of H$_2$CO $2_{12}\rightarrow 1_{11}$ in L1544 from Tafalla et al. [31]
Figure: Modelled results for H$_2$CO $2_{12}\rightarrow 1_{11}$ in L1544 with an abundance of $4\times 10^{-9}$.

Besides these low dipole moment molecules Tafalla et al. also collected data for high dipole moment molecules such as H$_2$CO, CS and HCO$+$. For these too the model can be run, again altering only the abundance. Unfortunately for these molecules the model does not work as well. Figure 7.9 shows the telescope data taken from Tafalla et al. [31] and figure 7.10 shows the equivalent modelled result. It is clear that the self absorption dip is nowhere near large enough in the modelled result. Although this may at first sight seem to be a major failing of the model an explanation for this can be found. In order to increase the size of the absorption dip it is necessary to have more cold material in the outer regions of the cloud. In the case of the N$_2$H$^+$ model only enough material was placed there to reproduce the N$_2$H$^+$ spectra for which data was available. The model cloud was therefore cut off at the 0.1pc distance. It is clear from the H$_2$CO data that the cloud in fact extends considerably further out and that this extended low excitation region has not been included in the model, hence the too weak absorption. Model output for the $1 \rightarrow 0$ transition of HCO+ for a standard cloud (solid line) and a much larger cloud (dashed line). In both cases the abundance was $5\times10^{-10}$ and the beamsize 54 $^{\prime \prime}$.  [l] This failing of the model is even more extreme for the HCO$+$ data where the absorption dip should be so large that it removes the red component completely. As can be seen from the solid line in figure 7.11 the standard model fails to do this. As a quick test of the above explanation, if the outer cloud is extended further then the absorption dip should increase. As the dashed line shows this is indeed the case, this line also has a peak intensity much closer to the 2.5K measured by the telescope. For this model the cloud had its radius increased to 0.2pc. All the parameter descriptions were held the same so that the inner 0.1pc is identical to that used previously except for the infall velocity which retained the same range of values but was spread over the 0.2pc rather than the 0.1pc previously. Clearly this has had a significant effect in the right direction. Further modelling would undoubtedly enable a fit to be found. Although, as might be expected, this change also increases the size of the absorption dip in the N$_2$H$^+$ models the increase here is not too large suggesting that it would not be too difficult to find a cloud description that fits both data sets. It may however be that in order to fit all the different molecules simultaneously some variation in the abundance with distance may be necessary (eg. as an extreme example if the N$_2$H$^+$ abundance were set to zero outside of 0.1pc then the above change to improve the HCO$+$ modelling would have no effect on the N$_2$H$^+$ model results).