




Next: An oblate model
Up: Modelling L1544
Previous: Required number of disks/cylinders
Looking at figure 7.3 it is clear from the general shape of the cloud that the most obvious simple
cloud models to consider are prolate or oblate spheroids. A prolate spheroid (a rugby ball shaped object)
would have its axis of symmetry aligned in the SE-NW direction. In order to simulate such a shape the hydrogen
distribution is described by
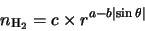 |
(7.1) |
where 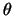 is given by
is given by
 where
where 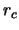 is the radial distance from the axis
of symmetry and
is the radial distance from the axis
of symmetry and 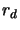 is the distance along the axis of symmetry. In figure 4.3 this is the
angle formed by the dashed line and the line labeled
is the distance along the axis of symmetry. In figure 4.3 this is the
angle formed by the dashed line and the line labeled 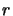 .
This enables two different power laws to be
specified, one along the major axis and one along the minor axis of the cloud. The
.
This enables two different power laws to be
specified, one along the major axis and one along the minor axis of the cloud. The
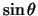 function then
varies smoothly between the two. For example with
function then
varies smoothly between the two. For example with 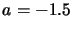 and
and 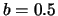 the hydrogen density drops off as
the hydrogen density drops off as
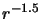 along the plane in the centre of the cloud that is perpendicular to the axis of symmetry and with
along the plane in the centre of the cloud that is perpendicular to the axis of symmetry and with
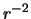 along the axis of symmetry. Lines radiating from the centre of the cloud but pointing elsewhere will
drop off with some power law between these two values. It is possible to
get quite easily an approximate fit to the line intensities with a cloud with a radius of order 0.1pc and a
distribution of H
along the axis of symmetry. Lines radiating from the centre of the cloud but pointing elsewhere will
drop off with some power law between these two values. It is possible to
get quite easily an approximate fit to the line intensities with a cloud with a radius of order 0.1pc and a
distribution of H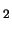 given by
given by
However, although this fits the peak intensities the modelled spectra to the NW and SE are clearly offset from the
telescope spectra. This offset is probably caused by rotation and can be corrected by making the cloud rotate
as a solid body with a speed of order 100 m s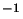 .
The problem with this is that it is rotation around the
cloud's minor axis. In other words this is end over end rotation of the major axis which is a probably an unrealistic situation. It
therefore seems clear that the cloud cannot be prolate.
.
The problem with this is that it is rotation around the
cloud's minor axis. In other words this is end over end rotation of the major axis which is a probably an unrealistic situation. It
therefore seems clear that the cloud cannot be prolate.





Next: An oblate model
Up: Modelling L1544
Previous: Required number of disks/cylinders
1999-04-12