




Next: Required number of disks/cylinders
Up: Radiative Transfer Modelling of
Previous: Limitations of the 'standard
The previous chapter has shown how it is possible to use the ASTRA program to predict the type of
observations that might be possible for a given object. However, the main use for the program is more likely
to be to help analyse data that has already been collected. There is only a fairly limited supply of objects
that have been observed at a suitable resolution for this. The necessary resolution can be obtained with
presently operating telescopes by considering objects that are as close to the Earth as possible. The closest
star formation region of significant size is the Taurus molecular cloud. It contains several objects that
have been studied in detail by various authors. The one that will be considered here is L1544. This has been
studied over many years by P. Myers and collaborators (eg. [23]). They have concluded that it is a cold dense core that
at present has no star in it but is "very advanced in its evolution toward the formation of one or more
low-mass stars" (Tafalla et. al. [31]). They have observed it in a wide variety of molecules
including CO, 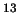 CO, C
CO, C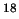 O, CS, C
O, CS, C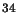 S, HCO
S, HCO ,
H
,
H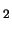 CO, C
CO, C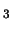 H
H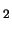 and N
and N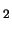 H
H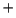 .
The N
.
The N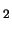 H
H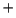 observations (see figure 7.2) were made with the Berkeley-Illinois-Maryland Array (BIMA) with a
observations (see figure 7.2) were made with the Berkeley-Illinois-Maryland Array (BIMA) with a
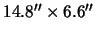 beam which
at the distance of L1554 corresponds to 0.01
beam which
at the distance of L1554 corresponds to 0.01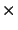 0.0045pc (2000
0.0045pc (2000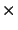 900 AU). This resolution is high
enough to resolve a sufficient number of positions across the cloud that detailed modelling can be attempted.
Model cloud used by Williams et al. [35]
[r]
900 AU). This resolution is high
enough to resolve a sufficient number of positions across the cloud that detailed modelling can be attempted.
Model cloud used by Williams et al. [35]
[r]
![\includegraphics*[trim=10.5cm 17.5cm 3.8cm 3cm ]{willsheet.ps}](img1254.gif) This has
been done by Williams et. al. [35]. They performed radiative transfer modelling of the cloud and
have been fairly successful in reproducing the observed line shapes. Their
model consisted of two sheets of material collapsing onto one another as shown in figure 7.1. The
front, low excitation layer falls towards the rear, high excitation layer producing the observed self absorbed
line shapes. The two layers share the same thickness, kinetic temperature, turbulent velocity and density
profiles but have different density peaks. The isodensity contours are taken to be elliptical in shape and
there is a velocity gradient parallel to the major axis. They take the temperature to be constant at 12K
across the entire cloud. The infall velocity is varied according to position to fit each spectrum individually.
The turbulent velocity is taken to be 0.22 km s
This has
been done by Williams et. al. [35]. They performed radiative transfer modelling of the cloud and
have been fairly successful in reproducing the observed line shapes. Their
model consisted of two sheets of material collapsing onto one another as shown in figure 7.1. The
front, low excitation layer falls towards the rear, high excitation layer producing the observed self absorbed
line shapes. The two layers share the same thickness, kinetic temperature, turbulent velocity and density
profiles but have different density peaks. The isodensity contours are taken to be elliptical in shape and
there is a velocity gradient parallel to the major axis. They take the temperature to be constant at 12K
across the entire cloud. The infall velocity is varied according to position to fit each spectrum individually.
The turbulent velocity is taken to be 0.22 km s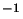 ,
this too being held constant over the entire cloud.
Across the plane of the cloud their hydrogen density is modelled by
,
this too being held constant over the entire cloud.
Across the plane of the cloud their hydrogen density is modelled by
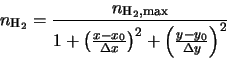
where 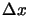 and
and 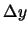 are the radii of the cloud in the
are the radii of the cloud in the 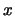 and
and 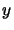 directions and
directions and 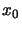 and
and 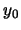 are the co-ordinates of the emission peak. There is also a velocity gradient that runs parallel to the major
axis in the cloud. This varies linearly at a rate of 3.8 km s
are the co-ordinates of the emission peak. There is also a velocity gradient that runs parallel to the major
axis in the cloud. This varies linearly at a rate of 3.8 km s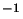 pc
pc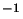 .
The results of this model can
be seen in figure 7.2. Clearly the model does provide quite good fits to most of the spectra
although in several cases the size of the absorption dip is under estimated by the model. There is extremely
good agreement for the peak intensity fitted on each spectra.
.
The results of this model can
be seen in figure 7.2. Clearly the model does provide quite good fits to most of the spectra
although in several cases the size of the absorption dip is under estimated by the model. There is extremely
good agreement for the peak intensity fitted on each spectra.
Nonetheless, despite this reasonably good fit the model suffers from several deficiencies the most major of
which is the lack of physical realism in the model. Clearly the cloud is unlikely to be made up out of two
layers, it is much more likely to be a oblate or prolate spheroid. The model also makes no attempt to fit a
global velocity structure to the cloud, instead it simply assigns a different infall velocity to each spectrum
to make it fit the data and a velocity gradient that varies only with position along the major axis. Whilst both of
these velocity structures provide a satisfactory fit to the data they are not based on any plausible physical
model of the cloud.
Despite these criticisms the model successfully provides an approximate description of the conditions in this cloud.
These can be used as a starting point for more sophisticated modelling using the ASTRA program. This is an ideal
test candidate for the ASTRA program as it is clearly non-spherically symmetric and has proven difficult to model
using traditional techniques. As a further complication the telescope beam and the cloud are not elongated in the
same direction. The FITS data cube containing the data shown in figure 7.2 was kindly provided by
Jonathan Williams and Philip Myers and will be modelled in detail in the next few sections.





Next: Required number of disks/cylinders
Up: Radiative Transfer Modelling of
Previous: Limitations of the 'standard
1999-04-12
![\includegraphics*[trim=10.5cm 17.5cm 3.8cm 3cm ]{willsheet.ps}](img1254.gif) This has
been done by Williams et. al. [35]. They performed radiative transfer modelling of the cloud and
have been fairly successful in reproducing the observed line shapes. Their
model consisted of two sheets of material collapsing onto one another as shown in figure 7.1. The
front, low excitation layer falls towards the rear, high excitation layer producing the observed self absorbed
line shapes. The two layers share the same thickness, kinetic temperature, turbulent velocity and density
profiles but have different density peaks. The isodensity contours are taken to be elliptical in shape and
there is a velocity gradient parallel to the major axis. They take the temperature to be constant at 12K
across the entire cloud. The infall velocity is varied according to position to fit each spectrum individually.
The turbulent velocity is taken to be 0.22 km s
This has
been done by Williams et. al. [35]. They performed radiative transfer modelling of the cloud and
have been fairly successful in reproducing the observed line shapes. Their
model consisted of two sheets of material collapsing onto one another as shown in figure 7.1. The
front, low excitation layer falls towards the rear, high excitation layer producing the observed self absorbed
line shapes. The two layers share the same thickness, kinetic temperature, turbulent velocity and density
profiles but have different density peaks. The isodensity contours are taken to be elliptical in shape and
there is a velocity gradient parallel to the major axis. They take the temperature to be constant at 12K
across the entire cloud. The infall velocity is varied according to position to fit each spectrum individually.
The turbulent velocity is taken to be 0.22 km s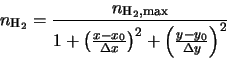
![\includegraphics*[trim=5cm 13.39cm 6cm 2.7cm ,scale=0.95]{willmodel.ps}](img1260.gif)
![\includegraphics*[trim=5.5cm 11cm 5.5cm 3.8cm , scale=0.95]{L1544.ps}](img1261.gif)