Using the Tcl/Tk Interface

The main Tcl Interface   [r] The interface is started by typing astra.tcl which brings up the window shown in figure 4.27. If this does not work it may be necessary to change the first line in the astra.tcl file to point to the correct location of the wish interpreter (note that very old versions of wish may not work correctly). The first of the three yellow buttons enables the setting up of the cylinder geometry within which the cloud is to be defined as well as the number of lines of sight that are to be used. The second yellow button enables the cloud parameters to be defined and the third button is the interface to previous runs. Pressing the green button writes the present selected model out to the input files and starts ASTRA. The button also runs ASTRA but rather than re-running the lambda iteration section again this just produces output using the solved cloud from the previous run. This enables several different types of output to be produced for a given cloud (eg. to simulate results from different telescopes).

An Option to Save the Run   [l] Once ASTRA is started a small window will almost immediately be displayed (as in figure 4.28) giving the option to save the run. If there is no intention to save the run the the button can be pressed straight away. However, if the run is to be saved then the button should only be pressed when ASTRA has finished (this is because pressing the button starts to transfer files which are only complete when ASTRA is finished). Finally, on the main window there is also a blue button which has no effect other than to kill off the Tcl windows (ie. all other files are left as they were).

Dealing with each of the three yellow buttons on the main interface in turn:

Method of distributing cylinders/disks in the cloud   [l] The ring geometry window consists of a top and side view display of the selected cloud, and panel on the right which enables the cylinder parameters to be altered. At the bottom is a statistics line which gives an idea of the size of the model being requested by listing the number of rings that will be in the cloud and the total number of lines of sight that will need to be calculated (this is simply the number of rings in the cloud multiplied by the number of lines of sight per ring). The parameters to be entered on the right are the number of cylinders and disks required for the model (note that for an even distribution there should be twice the number of disks as there are cylinders since the cylinders count from the centre and therefore cover only half the width of the cloud whereas the disks cover the entire height of the cloud). The value $hline$ (described in section 4.5.3) is a measure of the number of lines of sight. It must be a factor of four so a pulldown menu is provided with the first few possible options - although larger values are possible (this would entail only a simple modification to Tcl script) they will dramatically increase the run times. The next two pull down menus alter the distribution of the cylinders and disks throughout the cloud. The menus are simply labelled $x$, $x^2$, etc.; these define the function $f(x)$. The cylinders and disks are then distributed according to

$$c_i=\frac{f(x_i)}{f(r_{\rm c}-r_{\rm in})}(r_{\rm c}-r_{\rm in})+r_{\rm in}$$ (4.58)

where $c_i$ is the position of the $i^{\rm th}$ cylinder or disk,

$$x=\left( \frac{(r_{\rm c}-r_{\rm in})}{n_c-1}\right) \times i$$

$r_{\rm c}$ is the cloud radius/height, $r_{\rm in}$ is the inner cut off and $n_c$ is the number of cylinders/disks. The way this works is shown in figure 4.30. The x-axis shows the evenly spaced divisions between $r_{\rm in}$ and $r_{\rm c}$. These are then mapped via the function (in the diagram approximately a $x^{3}$ distribution) onto the actual spacings for the cylinders/disks. The distance $r_{\rm c}-r_{\rm in}$ is normalised so that the outer cylinder/disk of the cloud is in the same place for both distributions and the origin of function is taken as ( $r_{\rm in},r_{\rm in}$) for the same reason. Thus a value of $x$ will give an even distribution. Values of $x^2$, $x^{3}$ and $x^4$ increasingly weight the cylinders and disks towards the centre of the cloud. This is useful for models where the parameters are rapidly changing near the cloud centre but only change slowly further out. Finally, there are four entries defining the inner and outer edges of the model. Within the inner edge all model parameters are held constant at the level specified on the inner edge. This stops parameters such as the density reaching infinite values at the cloud centre. Upon exiting with the button the SHELL.DAT file is updated (see next section).

The parameter selection window shows a table of the presently selected parameter (this defaults to the relative molecular abundance at startup) at each disk and cylinder intersection. The pulldown menu at the centre bottom of the window changes the parameter shown. If desired the individual entries can be altered by hand. On startup the values are calculated using the formula displayed at the bottom. If the numbers are to be updated using this formula then the button should be pressed.

Adding an outflow   [l] To facilitate modelling outflows a simple model of an   outflow can be added. Pressing the button brings up the window shown in figure 4.32. This adds onto the already defined model parameters an outflow defined as shown in figure 4.33. Simply enter the required values and press . Selecting the button destroys the window and ignores any values that may have been entered. This outflow model is not in any way intended to be sophisticated but is only an attempt to provide a first approximation for an outflow. The individual fields for each parameter can of course be altered individually by hand if minor variations are required - otherwise for more major variations the outflow.f program can be substituted for a more complex version - this can be done without affecting the rest of the program.

Outflow definition   [r] As shown in Figure 4.33 the inner and outer walls of the outflow are described by two concentric hemispheres of radius $incirc$ and $outcirc$ closer to the centre of the cloud than $cenloc$. Further out from the centre of the cloud than the value given for `centre location' (hereafter $cenloc$) the outflow is considered to be parallel to the cylinders. Outflow only takes place within the cylinder bounded by $incirc$ and $outcirc$. Note the restriction imposed by the general requirement for 2-D symmetry - ie. that the outflow has to be perpendicular to the disks in the model. This means that (for example) when modelling a rotating disk with a bipolar outflow that the outflow has to be perpendicular to the disk. This restriction can only be overcome by conversion to a fully 3-D model. The outflow has a velocity $V_0r^n$ where $V_0$ is entered in the `Speed' entry and the value of $n$ is entered in the `Drop off' entry. $r$ is the distance from the cloud centre so, for example, a value of $n=1$ means the speed drops off linearly with distance from the cloud centre. The material in the outflow is assumed to `form' along the piece of the cloud axis that passes between the two hemispheres (this is shown by a slightly thicker section of line in figure 4.34). The amount of material flowing out down the outflow per unit time is constant and is entered in the `mass per second' field (hereafter $mps$).

Once all the parameters have been entered and the button pressed the fortran program `outflow.f' is started. This does the actual modification of the input files. It does this by considering all the intersections of disks and cylinders in turn so see if they are within the outflow or not. If the particular intersection being looked at is within the outflow then the outflow parameters at that point are calculated and added to the existing parameters at that point. As an example consider the intersection of a disk with co-ordinate $r_d$ and a cylinder with co-ordinate $r_{c}$. The program first checks to see if $r_d > cenloc$ and that $incirc < r_c < outcirc$. If these are true then the intersection lies in the region where the outflow is parallel to the cylinders.

   

Figure 4.34: Velocity field in outflow
Figure 4.35: Outflow intersections

For the region where the outflow is changing direction consider the triangles shown in figure 4.35 (the dashed line represents a disk at position $r_d$). First note that the lengths of the sides are related to the parameters entered by:

• ${\rm AC} = cenloc$
• ${\rm AD} = outcirc$
• ${\rm BC} = r_d$

From triangle ABD the distance BD is simply

$$BD=\sqrt{outcirc^2-\left(cenloc-\left\vert r_d\right\vert\right)^2}$$

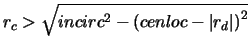( note the modulus sign which is needed to account for both parts of the outflow, above and below the cloud centre). If $r_{c}$ is less than this then the intersection point is within the outer edge of the outflow. If it also satisfies $r_c > \sqrt{incirc^2-\left(cenloc-\left\vert r_d\right\vert\right)^2}$then it lies outside the inner edge of the outflow. Therefore, if both these criteria are satisfied the intersection lies within the outflow. For those points within the outflow the hydrogen density is calculated and the velocity (radial and vertical).

The window for selecting from older stored runs consists of a section on the left listing the numbers of all runs that have been stored. Next to each number is a comment which is entered when the run is saved. Although up to 10 lines of comments can be entered per run only the first line is displayed here. The right half of the window then lists some of the more important parameters of the model selected (as default at start up the model selected is the last one saved). At the same time a GKS window will appear displaying the output from that run. Double clicking on the number for one of the previous runs will adopt the parameters from that run as those displayed in the right of the window and the output from that run will be displayed in the GKS window. The button will delete all the files associated with the currently selected run. The list is re-read by pressing the button which is necessary if new files have been calculated as they are not automatically added to the list. Only those parameters surrounded by depressed boxes can be altered in this window - the others can be altered only in other windows (eg. the cloud radius, ring numbers, etc. are altered in the already described section for setting up ring geometries (next to figure 4.31)). To alter the transitions that are to be output (and the positions at which they are to be output) press the button. This brings up the window shown in figure 4.37. A maximum of 5 transitions can be chosen and for each transition output can be generated at up to 6 positions. If the entries for the upper and lower transitions are the same (ie. $x \rightarrow x$) then that line is ignored. If a line has a valid transition then the number of non-zero pairs of co-ordinates plus one is taken to be the number of output positions (ie. the (0,0) position is always output) unless all co-ordinate positions are zero in which case it is assumed that just one output is required at the (0,0) position.

  

Figure 4.37: Altering the output

Hardcopy   [l] If a hardcopy of the selected model output is required then press the button. This brings up the window shown in figure 4.38 which has one pull down menu. Selecting `xw' (the default) prints to the Xwindow, `ps_l' produces a landscape postscript page and `ps_p' a portrait postscript page. The final choice of `epsf_p' (for encapsulated postscript) brings up another window (shown in figure 4.39) that is used to enter the required dimensions for the epsf output. Selecting epsf size   [r] Once the required output has been selected press the button. This prints the postscript file to disk (except for the `xw' option which only draws on the screen). Once the postscript file has been written to disk a button appears giving the option to send this file to the printer. Note that this works simply by issuing the command 'lp gks74.ps' so in order for this to work the PGPLOT interface must write postscript file to this file name. This will only occur if the file does not already exist so the program first issues the command `rm gks74.ps'. This of course deletes any file that may previously have existed under this name.

Draw a position velocity diagram   [l] For runs where output was generated for a cut across the cloud a position velocity diagram can be generated by pressing the button which brings up figure 4.40. Here it is simply necessary to select the transition for which the p-v diagram is required and select the type of output required (this operates in the same way as the hardcopy generation described above). This then calls the posvel.f program which actually produces the position velocity diagram and displays it either on the screen or saves it as an eps file.

Produce a grid spectra map   [l] The final option is to produce a grid spectra map. This is done by pressing the button which brings up figure 4.41. There are two options here, represented by the and buttons. Max mode detects the extreme positions for which
model data was calculated and produces a grid map that exactly fits these positions (note that the calculated positions must be evenly spaced and must match the value entered in the grid spacing box). Custom mode allows the user to define the size of the grid by giving in the left and bottom edge co-ordinates and then entering the number of positions. The number of positions times the grid spacing then gives the width of the map. Finally the required output type can be selected by clicking on one of the radio buttons. If an eps output is selected the size of the output must also be specified.