




Next: Observing Star Formation Regions
Up: Star Formation
Previous: Classification of Protostellar Objects
Of fundamental importance for studying the development of a protostar through these various stages
is the ability to deduce the internal parameters (ie. density, temperature, etc.) through external
observations. The only way of doing this for objects that are so far away from the Earth is by studying the
radiation they emit. Radiation at different frequencies will originate at different positions in a
cloud, therefore by observing a given cloud at many different wavelengths it is, in theory, possible to deduce
the internal structure. This thesis is concerned with one method of doing this, namely the use of radiative
transfer modelling. The idea here is that the parameters in a cloud are assumed and then by some method the
radiation emitted from the cloud is calculated. By varying the parameters in the cloud it should then be
possible to reproduce observations seen by a telescope. Although simple in theory this is in fact a rather
difficult problem, mainly due to the very large parameter space that a gas cloud covers. Nonetheless over
the last two decades several computer programs have been written that attempt to do this. The main methods
used in these programs will be described in chapter 3.
Of particular interest in the study of star formation regions are the relative sizes of the envelope and any
circumstellar disk with respect to the mass of the star being formed. Radiative transfer modelling aims to
show how the matter is distributed and what if any dynamical changes are taking place (eg. rotation and
collapse). These results can then be compared with chemical models of protostellar clouds to attempt to place
the objects observed on an evolutionary sequence.
Example of modelling with a spherically symmetric radiative transfer model (see text for
explanation).
[l]
![\includegraphics[scale=0.5]{andy1.eps}](img56.gif) Thus far almost all radiative transfer models written have been forced to assume spherical symmetry of the
objects being modelled. This assumption makes for much easier programming and, more importantly, makes the
models much less computing intensive. Prior to the advent of computer chips capable of running at clock speeds
of many hundred MHz it was not practical to consider writing any more complex models. Despite these draw backs
considerable success has been had using spherically symmetric radiative transfer models. As an example of this
figure 1.4 shows observations (solid lines) of the cloud G34.3+0.2 taken from Little et
al. [19]. In order, from the bottom upwards the spectra are C
Thus far almost all radiative transfer models written have been forced to assume spherical symmetry of the
objects being modelled. This assumption makes for much easier programming and, more importantly, makes the
models much less computing intensive. Prior to the advent of computer chips capable of running at clock speeds
of many hundred MHz it was not practical to consider writing any more complex models. Despite these draw backs
considerable success has been had using spherically symmetric radiative transfer models. As an example of this
figure 1.4 shows observations (solid lines) of the cloud G34.3+0.2 taken from Little et
al. [19]. In order, from the bottom upwards the spectra are C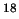 O J=2
O J=2
 1 and
1 and
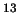 CO J=1
CO J=1
 0, J=2
0, J=2
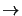 1 and J=3
1 and J=3
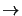 2. The dashed lines are the modelled
results from a spherically symmetric radiative transfer model. Despite the fact that other observations of
G34.3+0.2 show it to
be only roughly spherically symmetric these models clearly do a very good approximation of the actual observed
lines. The line shapes are a result of a collapsing cloud with the outer cooler layers self absorbing the
emitting hotter material in the core. The self absorption dip is not centred at the line centre due to the
Doppler shifting of the colder infalling material in the outer regions relative to the slow moving hot material near the cloud
centre.
2. The dashed lines are the modelled
results from a spherically symmetric radiative transfer model. Despite the fact that other observations of
G34.3+0.2 show it to
be only roughly spherically symmetric these models clearly do a very good approximation of the actual observed
lines. The line shapes are a result of a collapsing cloud with the outer cooler layers self absorbing the
emitting hotter material in the core. The self absorption dip is not centred at the line centre due to the
Doppler shifting of the colder infalling material in the outer regions relative to the slow moving hot material near the cloud
centre.
Despite this obvious success at modelling G34 there are many objects that can clearly not be modelled with the
restriction of spherically symmetry. This includes such important objects as disks and filaments as well as
any object which exhibits rotation or any other kind of motion that is non-spherically symmetric -
specifically bi-polar outflows fall into this category. In order to be able to model such objects a radiative
transfer program is needed that requires less symmetry in the objects being modelled. This thesis will present
a detailed description of such a program. The question immediately arises as to what kind of additional
complexity should be included in such a program. It is important to not make the problem too complex as
additional complexity generally involves more computing power and it is very easy to write a program that
takes too long to run to be useful. Since most of the objects that are seen have 2-D symmetry (ie. have one
axis of symmetry) this is one immediate simplification over a fully 3-D model. 2-D models can deal with disks,
cylinders, filaments and outflows such as the examples shown in figures 1.1 & 1.2 (as long as the outflow lines up with the axis of symmetry). The method and
implementation of such a program is described in chapter 4.
With the advent of larger submillimeter telescopes and more sensitive receivers in the 1980's the opportunity
to detect many more types of molecules has become available. These molecules (eg. formaldehyde H CO) are
much rarer that the more common molecules such as CO and need these large telescopes to be detected with
sufficient signal-to-noise to be able to glean useful data from the line shape. The STENHOLM
program1.6 that was used to produce figure 1.4 was only
capable of handling linear molecules (eg. CO or HCO+). As a first step this program has been modified to
enable it to handle all molecules for which the necessary collision rate data is available. This will be
described in section 4.2 (with a general introduction to the methods used for radiative transfer
modelling presented in chapter 3). This ability to model rarer molecules is useful when trying
to fit the observed objects with chemical models since the more molecules that can be fitted in such models
the more confident one can be in the result.
CO) are
much rarer that the more common molecules such as CO and need these large telescopes to be detected with
sufficient signal-to-noise to be able to glean useful data from the line shape. The STENHOLM
program1.6 that was used to produce figure 1.4 was only
capable of handling linear molecules (eg. CO or HCO+). As a first step this program has been modified to
enable it to handle all molecules for which the necessary collision rate data is available. This will be
described in section 4.2 (with a general introduction to the methods used for radiative transfer
modelling presented in chapter 3). This ability to model rarer molecules is useful when trying
to fit the observed objects with chemical models since the more molecules that can be fitted in such models
the more confident one can be in the result.
Before delving into the detailed description of radiative transfer modelling an overview of some of the theory
behind molecular line emission will be presented. This will also include a brief description of the design and operation of
the telescopes used to detect this emission together with some of the basic methods of data reduction.





Next: Observing Star Formation Regions
Up: Star Formation
Previous: Classification of Protostellar Objects
1999-04-12
![\includegraphics[scale=0.5]{andy1.eps}](img56.gif) Thus far almost all radiative transfer models written have been forced to assume spherical symmetry of the
objects being modelled. This assumption makes for much easier programming and, more importantly, makes the
models much less computing intensive. Prior to the advent of computer chips capable of running at clock speeds
of many hundred MHz it was not practical to consider writing any more complex models. Despite these draw backs
considerable success has been had using spherically symmetric radiative transfer models. As an example of this
figure 1.4 shows observations (solid lines) of the cloud G34.3+0.2 taken from Little et
al. [19]. In order, from the bottom upwards the spectra are C
Thus far almost all radiative transfer models written have been forced to assume spherical symmetry of the
objects being modelled. This assumption makes for much easier programming and, more importantly, makes the
models much less computing intensive. Prior to the advent of computer chips capable of running at clock speeds
of many hundred MHz it was not practical to consider writing any more complex models. Despite these draw backs
considerable success has been had using spherically symmetric radiative transfer models. As an example of this
figure 1.4 shows observations (solid lines) of the cloud G34.3+0.2 taken from Little et
al. [19]. In order, from the bottom upwards the spectra are C