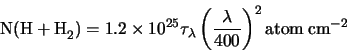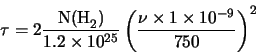



Next: The Tcl/Tk interface
Up: A Generalised 2-D Radiative
Previous: Outputting the Results
A Modification to Allow Modelling of Dust
Due to the modularisation of the program it is easy to cut out and replace some of the individual elements of the
program. One reason for doing this is to enable the modelling of other physical processes besides molecular
line excitation whilst still using the same 2-D geometric structure. Other processes that might be of interest are
line emission in other galaxies and processes associated with dust. Both of these would entail considerable
work in replacing the present lambda iteration section with an appropriate new section. However, there is one
fairly easy modification that enables dust continuum emission from star formation regions to be approximately
modelled.
A well known model for continuum dust emission from grains is that of Hildebrand [13]. This can be
used to approximate the
submillimetre dust emission in terms of the amount of hydrogen present in a cloud. The details of this model will
not be presented here but the result is that optical depth is related to the amount of hydrogen present by
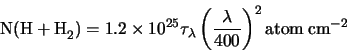 |
(4.56) |
where 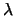 is the wavelength (in
is the wavelength (in 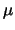 m) for which the optical depth is desired. Once the optical depth is known the
emissivity coefficient can be calculated from
m) for which the optical depth is desired. Once the optical depth is known the
emissivity coefficient can be calculated from
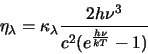 |
(4.57) |
provided
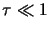 (this condition means the optical depth of each segment on a line of sight must be small).
These two lines can be used to replace the lambda iteration section of the ASTRA program since once these
values are known for every ring in the cloud the output section can calculate the intensity that a telescope
would see if it were pointed at the cloud. This is in fact considerably easier than for molecular line emission
since there is no velocity information required.
(this condition means the optical depth of each segment on a line of sight must be small).
These two lines can be used to replace the lambda iteration section of the ASTRA program since once these
values are known for every ring in the cloud the output section can calculate the intensity that a telescope
would see if it were pointed at the cloud. This is in fact considerably easier than for molecular line emission
since there is no velocity information required.
It should be noted that this is not a global solution of the radiative transfer equation in the way that the
ASTRA program does for spectral lines. Instead it is simply a computation of the radiation intensity along a line of
sight emitted by dust that has a specified density and temperature distribution.
The program that implements this (lesdust.f) is in fact considerably simpler than the ASTRA program. The entire
lambda iteration routine is replaced by just two lines representing
equations 4.56 & 4.57. Note that equation 4.56 is actually written
as
The initial factor of two is because the N(H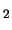 )
value counts the number of molecules of H
)
value counts the number of molecules of H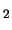 which each
contain 2 atoms of hydrogen. The 750 term at the end is now in Gigahertz (ie. the 400
which each
contain 2 atoms of hydrogen. The 750 term at the end is now in Gigahertz (ie. the 400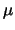 m in
equation 4.56 is converted to 750GHz) whereas
m in
equation 4.56 is converted to 750GHz) whereas 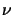 is in Hertz, hence the
factor of
is in Hertz, hence the
factor of 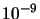 .
The value of
.
The value of 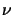 for which output is required is entered in a modified version of the MODELDATA.DAT input file. The program will
calculate the emission for various positions on the cloud and thereby produce a dust emission map of the
object. A grey scale map is then produced using PGPLOT which can be overlaid with contours if desired to enable
easy comparison with observed dust maps (such as those produced by SCUBA on the JCMT).
for which output is required is entered in a modified version of the MODELDATA.DAT input file. The program will
calculate the emission for various positions on the cloud and thereby produce a dust emission map of the
object. A grey scale map is then produced using PGPLOT which can be overlaid with contours if desired to enable
easy comparison with observed dust maps (such as those produced by SCUBA on the JCMT).
Since only one line in the program is used to specify the emissivity law for the dust the program can easily be
modified to run for dust emission laws other than that of Hildebrand.




Next: The Tcl/Tk interface
Up: A Generalised 2-D Radiative
Previous: Outputting the Results
1999-04-12